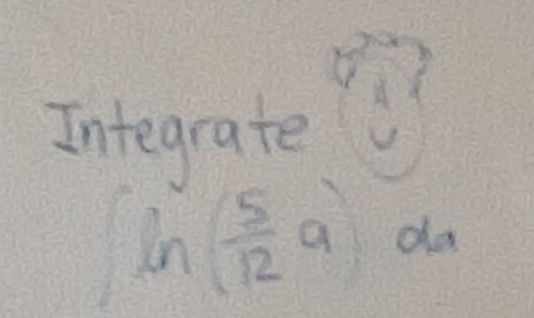AI tutor
Full solution
Q. Integrate
- Set : We are asked to integrate the natural logarithm function with respect to . The integral of with respect to is , where is the constant of integration. We will use this formula to integrate with respect to .
- Substitute and : First, let's set . This means that , and thus . We will substitute for and for in the integral.
- Apply integration formula: The integral becomes . We can pull the constant outside the integral, so it becomes .
- Simplify the expression: Now we apply the integration formula for , which is . The integral of with respect to is .
- Final answer: Substituting back in for , we get \frac{\(12\)}{\(5\)} \cdot \left(\frac{\(5\)}{\(12\)}a\ln\left(\frac{\(5\)}{\(12\)}a\right) - \frac{\(5\)}{\(12\)}a\right) + C.
- Final answer: Substituting back in for \(u, we get . Simplify the expression by multiplying through by . This gives us , where is a new constant of integration that absorbs the factor.
- Final answer: Substituting back in for , we get . Simplify the expression by multiplying through by . This gives us , where is a new constant of integration that absorbs the factor. The final answer is , where is the constant of integration.
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help