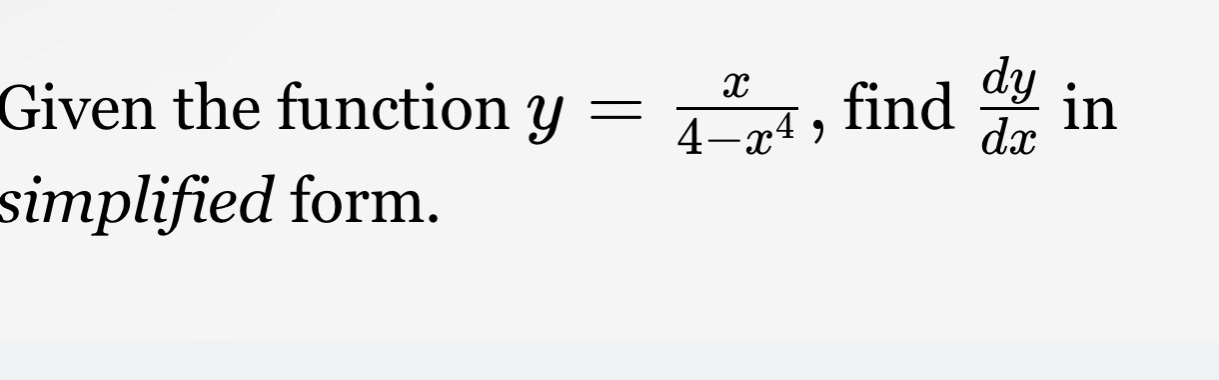Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the function
y=(x)/(4-x^(4)), find
(dy)/(dx) in simplified form.

Given the function $y=\frac{x}{4-x^{4}}$ , find $\frac{dy}{dx}$ in simplified form.

View step-by-step help

View step-by-step help

Sin, cos, and tan of special angles

Full solution

Q. Given the function

y=\frac{x}{4-x^{4}}

, find

\frac{dy}{dx}

in simplified form.

Identify Function and Need: Identify the function and the need to differentiate with respect to $x$ . $\newline$ Function: $y = \frac{x}{4 - x^4}$ $\newline$ We need to find $\frac{dy}{dx}$ .
Apply Quotient Rule: Apply the quotient rule for differentiation, which is $(v'u - uv') / (v^2)$ where $u = x$ and $v = 4 - x^4$ . Differentiate $u$ : $u' = 1$ Differentiate $v$ : $v' = -4x^3$ (using the power rule) Now apply the quotient rule.
Substitute Derivatives: Substitute the derivatives into the quotient rule formula. $\newline$ $\frac{dy}{dx} = \frac{(4 - x^4)(1) - (x)(-4x^3)}{(4 - x^4)^2}$ $\newline$ Simplify the numerator: $(4 - x^4 + 4x^4) = 4 + 3x^4$

More problems from Sin, cos, and tan of special angles

Question

Marco's class is painting a mural on the side of their school. The mural covers a

3 \frac{1}{2} \mathrm{~m}

high, rectangular wall. It has an area of

28 \mathrm{~m}^{2}

\newline

What is the length of the mural?

\newline

Posted 10 months ago

Question

A cup of hot coffee has been left to cool in a room with an ambient temperature of

21^{\circ} \mathrm{C}

\newline

The relationship between the elapsed time,

m

, in minutes, since the coffee was left to cool, and the temperature of the coffee,

T

{ }^{\circ} \mathrm{C}

, is modeled by the following function.

\newline

T(m)=21+74 \cdot 10^{-0.03 m}

\newline

What will the temperature of the coffee be after

10

\newline

Round your answer, if necessary, to the nearest hundredth.

\newline

{ }^{\circ} C

Posted 10 months ago

Question

Takumi plants a tree in his backyard and studies how the number of branches grows over time.

\newline

He predicts that the relationship between

N

, the number of branches on the tree, and

t

, the elapsed time, in years, since the tree was planted can be modeled by the following equation.

\newline

N=5 \cdot 10^{0.3 t}

\newline

According to Takumi's model, in how many years will the tree have

100

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 10 months ago

Question

g(x)=2^{x}

\newline

Can we use the mean value theorem to say the equation

g^{\prime}(x)=16

has a solution where

3<x<5

\newline

1

\newline

(A) No, since the function is not differentiable on that interval.

\newline

(B) No, since the average rate of change of

g

over the interval

3 \leq x \leq 5

1 \overline{6}

\newline

(C) Yes, both conditions for using the mean value theorem have been met.

Posted 9 months ago

Question

\frac{d}{d x}\left(\frac{3 x^{2}-1}{x-2}\right)=

Posted 9 months ago

Question

\frac{d y}{d t}=2 t+3 \text { and } y(1)=6

\newline

t

y=0

\newline

Choose all answers that apply:

\newline

t=-1

\newline

t=-3

\newline

t=0

\newline

t=-4

\newline

t=1

\newline

t=-2

Posted 9 months ago

Question

\frac{d}{d x}\left(x^{\frac{3}{4}}\right)=

Posted 9 months ago

Question

y=x^{13}

\newline

\frac{d y}{d x}=

Posted 9 months ago

Question

y=x^{10}

\newline

\frac{d y}{d x}=

Posted 9 months ago

Question

\frac{d}{d x}\left[x^{6}\right]=

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant