Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Marco's class is painting a mural on the side of their school. The mural covers a
3(1)/(2)m high, rectangular wall. It has an area of
28m^(2).
What is the length of the mural?
m

Marco's class is painting a mural on the side of their school. The mural covers a $3 \frac{1}{2} \mathrm{~m}$ high, rectangular wall. It has an area of $28 \mathrm{~m}^{2}$ . $\newline$ What is the length of the mural? $\newline$ m

View step-by-step help

View step-by-step help

Pythagorean Theorem and its converse

Full solution

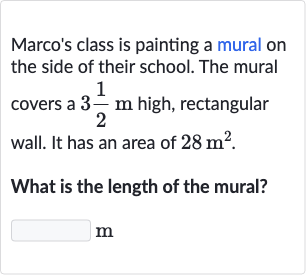
Q. Marco's class is painting a mural on the side of their school. The mural covers a

3 \frac{1}{2} \mathrm{~m}

high, rectangular wall. It has an area of

28 \mathrm{~m}^{2}

.

\newline

What is the length of the mural?

\newline

m

Identify Problem & Values: Understand the problem and identify the given values. $\newline$ We are given the height of the mural, which is $3.5$ meters ( $3\frac{1}{2}m$ ), and the area of the mural, which is $28$ square meters ( $28m^{2}$ ). We need to find the length of the mural.
Use Area Formula: Use the formula for the area of a rectangle to find the length. $\newline$ The area of a rectangle is given by the formula $\text{Area} = \text{Length} \times \text{Height}$ . We can rearrange this formula to solve for the length: $\text{Length} = \frac{\text{Area}}{\text{Height}}$ .
Calculate Length: Plug in the given values and calculate the length. $\newline$ Length = $\frac{28m^{2}}{3.5m}$
Perform Division: Perform the division to find the length. $\newline$ Length = $28 \div 3.5$ $\newline$ Length = $8$
Check Calculation: Check the calculation for any mathematical errors. $\newline$ Recheck the division: $28 \div 3.5 = 8$ . There are no mathematical errors in the calculation.

More problems from Pythagorean Theorem and its converse

Question

A cup of hot coffee has been left to cool in a room with an ambient temperature of

21^{\circ} \mathrm{C}

\newline

The relationship between the elapsed time,

m

, in minutes, since the coffee was left to cool, and the temperature of the coffee,

T

{ }^{\circ} \mathrm{C}

, is modeled by the following function.

\newline

T(m)=21+74 \cdot 10^{-0.03 m}

\newline

What will the temperature of the coffee be after

10

\newline

Round your answer, if necessary, to the nearest hundredth.

\newline

{ }^{\circ} C

Posted 7 months ago

Question

Takumi plants a tree in his backyard and studies how the number of branches grows over time.

\newline

He predicts that the relationship between

N

, the number of branches on the tree, and

t

, the elapsed time, in years, since the tree was planted can be modeled by the following equation.

\newline

N=5 \cdot 10^{0.3 t}

\newline

According to Takumi's model, in how many years will the tree have

100

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 7 months ago

Question

g(x)=2^{x}

\newline

Can we use the mean value theorem to say the equation

g^{\prime}(x)=16

has a solution where

3<x<5

\newline

1

\newline

(A) No, since the function is not differentiable on that interval.

\newline

(B) No, since the average rate of change of

g

over the interval

3 \leq x \leq 5

1 \overline{6}

\newline

(C) Yes, both conditions for using the mean value theorem have been met.

Posted 7 months ago

Question

\frac{d}{d x}\left(\frac{3 x^{2}-1}{x-2}\right)=

Posted 7 months ago

Question

\frac{d y}{d t}=2 t+3 \text { and } y(1)=6

\newline

t

y=0

\newline

Choose all answers that apply:

\newline

t=-1

\newline

t=-3

\newline

t=0

\newline

t=-4

\newline

t=1

\newline

t=-2

Posted 7 months ago

Question

\frac{d}{d x}\left(x^{\frac{3}{4}}\right)=

Posted 7 months ago

Question

y=x^{13}

\newline

\frac{d y}{d x}=

Posted 7 months ago

Question

y=x^{10}

\newline

\frac{d y}{d x}=

Posted 7 months ago

Question

\frac{d}{d x}\left[x^{6}\right]=

Posted 7 months ago

Question

\frac{2 x+8}{5}=\frac{3 x+2}{6}

Posted 24 hours ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant