Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(dy)/(dt)=2t+3" and "y(1)=6
What is
t when
y=0 ?
Choose all answers that apply:
A
t=-1
B
t=-3
C
t=0
D
t=-4
ㅌ
t=1
F
t=-2

$\frac{d y}{d t}=2 t+3 \text { and } y(1)=6$ $\newline$ What is $t$ when $y=0$ ? $\newline$ Choose all answers that apply: $\newline$ (A) $t=-1$ $\newline$ (B) $t=-3$ $\newline$ (C) $t=0$ $\newline$ (D) $t=-4$ $\newline$ (E) $t=1$ $\newline$ (F) $t=-2$

View step-by-step help

View step-by-step help

Solve complex trigonomentric equations

Full solution

Q.

\frac{d y}{d t}=2 t+3 \text { and } y(1)=6

\newline

What is

t

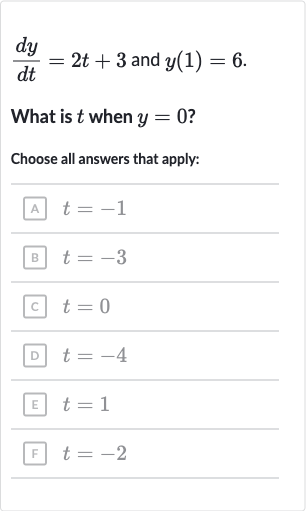
when

y=0

?

\newline

Choose all answers that apply:

\newline

(A)

t=-1

\newline

(B)

t=-3

\newline

(C)

t=0

\newline

(D)

t=-4

\newline

(E)

t=1

\newline

(F)

t=-2

Integrate Equation: Given the differential equation $\frac{dy}{dt} = 2t + 3$ and the initial condition $y(1) = 6$ , we want to find the value of $t$ when $y = 0$ . To do this, we need to integrate the differential equation to find the general solution for $y(t)$ .
Find General Solution: Integrate the right-hand side of the equation with respect to $t$ to find $y(t)$ . The integral of $2t$ with respect to $t$ is $t^2$ , and the integral of $3$ with respect to $t$ is $3t$ . So, the integral of $\frac{dy}{dt} = 2t + 3$ is $y(t) = t^2 + 3t + C$ , where $y(t)$ $0$ is the constant of integration.
Use Initial Condition: Use the initial condition $y(1) = 6$ to find the value of the constant $C$ . Plugging in the values, we get $6 = 1^2 + 3(1) + C$ , which simplifies to $6 = 1 + 3 + C$ . Therefore, $C = 6 - 4 = 2$ .
Write Particular Solution: Now that we have the constant, we can write the particular solution for $y(t)$ as $y(t) = t^2 + 3t + 2$ .
Set Equation Equal to Zero: To find the value of $t$ when $y = 0$ , we set the equation $y(t) = t^2 + 3t + 2$ equal to $0$ and solve for $t$ . This gives us the quadratic equation $t^2 + 3t + 2 = 0$ .
Factor Quadratic Equation: Factor the quadratic equation to find the values of $t$ . The equation $t^2 + 3t + 2 = 0$ factors into $(t + 1)(t + 2) = 0$ .
Solve for $t$ : Set each factor equal to zero and solve for $t$ . This gives us $t + 1 = 0$ and $t + 2 = 0$ , which means $t = -1$ and $t = -2$ are the solutions.
Check Answer Choices: We can now check the answer choices to see which ones apply. The correct answers are A $t = -1$ and F $t = -2$ .

More problems from Solve complex trigonomentric equations

Question

Marco's class is painting a mural on the side of their school. The mural covers a

3 \frac{1}{2} \mathrm{~m}

high, rectangular wall. It has an area of

28 \mathrm{~m}^{2}

\newline

What is the length of the mural?

\newline

Posted 4 months ago

Question

A cup of hot coffee has been left to cool in a room with an ambient temperature of

21^{\circ} \mathrm{C}

\newline

The relationship between the elapsed time,

m

, in minutes, since the coffee was left to cool, and the temperature of the coffee,

T

{ }^{\circ} \mathrm{C}

, is modeled by the following function.

\newline

T(m)=21+74 \cdot 10^{-0.03 m}

\newline

What will the temperature of the coffee be after

10

\newline

Round your answer, if necessary, to the nearest hundredth.

\newline

{ }^{\circ} C

Posted 4 months ago

Question

Takumi plants a tree in his backyard and studies how the number of branches grows over time.

\newline

He predicts that the relationship between

N

, the number of branches on the tree, and

t

, the elapsed time, in years, since the tree was planted can be modeled by the following equation.

\newline

N=5 \cdot 10^{0.3 t}

\newline

According to Takumi's model, in how many years will the tree have

100

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 4 months ago

Question

g(x)=2^{x}

\newline

Can we use the mean value theorem to say the equation

g^{\prime}(x)=16

has a solution where

3<x<5

\newline

1

\newline

(A) No, since the function is not differentiable on that interval.

\newline

(B) No, since the average rate of change of

g

over the interval

3 \leq x \leq 5

1 \overline{6}

\newline

(C) Yes, both conditions for using the mean value theorem have been met.

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{x^{2}-x+5}{4 x-1}\right)=

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{2 x^{2}+x-3}{2 x+7}\right)=

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{3 x^{2}-1}{x-2}\right)=

Posted 3 months ago

Question

\frac{d}{d x}\left(x^{\frac{3}{4}}\right)=

Posted 3 months ago

Question

y=x^{13}

\newline

\frac{d y}{d x}=

Posted 3 months ago

Question

6\left(\frac{1}{2}w-\frac{3}{4}\right)

Posted 23 hours ago