Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

y=x^(13)

(dy)/(dx)=

$y=x^{13}$ $\newline$ $\frac{d y}{d x}=$

View step-by-step help

View step-by-step help

Csc, sec, and cot of special angles

Full solution

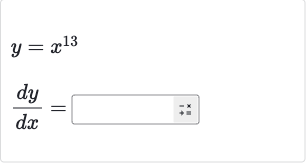
Q.

y=x^{13}

\newline

\frac{d y}{d x}=

Apply Power Rule: To find the derivative of $y$ with respect to $x$ , we will use the power rule for differentiation. The power rule states that if $y = x^n$ , then the derivative $\frac{dy}{dx}$ is $n \cdot x^{(n-1)}$ .
Calculate Derivative: Applying the power rule to $y = x^{13}$ , we get $\frac{dy}{dx} = 13 \cdot x^{13-1} = 13 \cdot x^{12}$ .
Final Result: There are no further simplifications needed, so we have found the derivative.

More problems from Csc, sec, and cot of special angles

Question

Marco's class is painting a mural on the side of their school. The mural covers a

3 \frac{1}{2} \mathrm{~m}

high, rectangular wall. It has an area of

28 \mathrm{~m}^{2}

\newline

What is the length of the mural?

\newline

Posted 8 months ago

Question

A cup of hot coffee has been left to cool in a room with an ambient temperature of

21^{\circ} \mathrm{C}

\newline

The relationship between the elapsed time,

m

, in minutes, since the coffee was left to cool, and the temperature of the coffee,

T

{ }^{\circ} \mathrm{C}

, is modeled by the following function.

\newline

T(m)=21+74 \cdot 10^{-0.03 m}

\newline

What will the temperature of the coffee be after

10

\newline

Round your answer, if necessary, to the nearest hundredth.

\newline

{ }^{\circ} C

Posted 8 months ago

Question

Takumi plants a tree in his backyard and studies how the number of branches grows over time.

\newline

He predicts that the relationship between

N

, the number of branches on the tree, and

t

, the elapsed time, in years, since the tree was planted can be modeled by the following equation.

\newline

N=5 \cdot 10^{0.3 t}

\newline

According to Takumi's model, in how many years will the tree have

100

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 8 months ago

Question

g(x)=2^{x}

\newline

Can we use the mean value theorem to say the equation

g^{\prime}(x)=16

has a solution where

3<x<5

\newline

1

\newline

(A) No, since the function is not differentiable on that interval.

\newline

(B) No, since the average rate of change of

g

over the interval

3 \leq x \leq 5

1 \overline{6}

\newline

(C) Yes, both conditions for using the mean value theorem have been met.

Posted 7 months ago

Question

\frac{d}{d x}\left(\frac{3 x^{2}-1}{x-2}\right)=

Posted 7 months ago

Question

\frac{d y}{d t}=2 t+3 \text { and } y(1)=6

\newline

t

y=0

\newline

Choose all answers that apply:

\newline

t=-1

\newline

t=-3

\newline

t=0

\newline

t=-4

\newline

t=1

\newline

t=-2

Posted 7 months ago

Question

\frac{d}{d x}\left(x^{\frac{3}{4}}\right)=

Posted 7 months ago

Question

y=x^{10}

\newline

\frac{d y}{d x}=

Posted 7 months ago

Question

\frac{d}{d x}\left[x^{6}\right]=

Posted 7 months ago

Question

\newline

A fun house mirror distorts the image it reflects. Objects reflected in the mirror appear

1 . \overline{3}

times taller. When a five-foot-tall person looks in the mirror, how tall does he appear?

\newline

\square

\square

Posted 16 minutes ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant