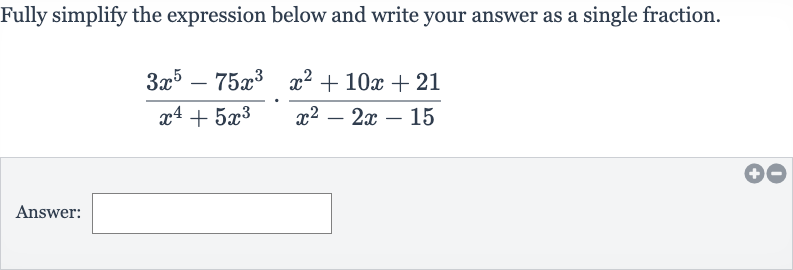
Fully simplify the expression below and write your answer as a single fraction. (3x^(5)-75x^(3))/(x^(4)+5x^(3))*(x^(2)+10 x+21)/(x^(2)-2x-15) Answer:

Question

Fully simplify the expression below and write your answer as a single fraction.  (3x^(5)-75x^(3))/(x^(4)+5x^(3))*(x^(2)+10 x+21)/(x^(2)-2x-15) Answer:

Bytelearn · Accepted Answer

Identify and Factor Expression: Identify the expression to be simplified and factor each part where possible. The expression is (3x^(5)-75x^(3))/(x^(4)+5x^(3))*(x^(2)+10x+21)/(x^(2)-2x-15). Factor out common terms in the numerator and denominator.Factor Numerator: Factor the numerator 3x^(5)-75x^(3) by taking out the common factor of 3x^3. 3x^(5)-75x^(3) = 3x^3(x^2-25). Notice that x^2-25 is a difference of squares and can be factored further.Factor Denominator: Factor x^2-25 into (x+5)(x-5). So, 3x^(5)-75x^(3) becomes 3x^3(x+5)(x-5).Factor x^2-25: Factor the denominator x^(4)+5x^(3) by taking out the common factor of x^3. x^(4)+5x^(3) = x^3(x+5).Factor x^2+10x+21: Factor the numerator x^(2)+10x+21 by finding two numbers that multiply to 21 and add to 10. These numbers are 3 and 7, so x^(2)+10x+21 factors into (x+3)(x+7).Factor x^2-2x-15: Factor the denominator x^(2)-2x-15 by finding two numbers that multiply to -15 and add to -2. These numbers are -5 and 3, so x^(2)-2x-15 factors into (x-5)(x+3).Rewrite with Factored Parts: Now rewrite the original expression with all the factored parts: (3x^3(x+5)(x-5))/(x^3(x+5)) * ((x+3)(x+7))/((x-5)(x+3)).Cancel Common Factors: Cancel out the common factors in the numerator and denominator. The (x+5) and x^3 terms cancel out, as well as one (x+3) term. The simplified expression is now (3(x-5))/(1) * (x+7)/(x-5).Cancel (x-5) Terms: Cancel out the common (x-5) terms in the numerator and denominator. The simplified expression is now 3 * (x+7).Final Simplified Expression: Since there are no more common factors, the expression is fully simplified. The final simplified expression is 3x+21.

Fully simplify the expression below and write your answer as a single fraction. $\newline$ $\frac{3 x^{5}-75 x^{3}}{x^{4}+5 x^{3}} \cdot \frac{x^{2}+10 x+21}{x^{2}-2 x-15}$ $\newline$ Answer:

Full solution

More problems from Operations with rational exponents

Related topics

Fully simplify the expression below and write your answer as a single fraction.\newline3x5−75x3x4+5x3⋅x2+10x+21x2−2x−15 \frac{3 x^{5}-75 x^{3}}{x^{4}+5 x^{3}} \cdot \frac{x^{2}+10 x+21}{x^{2}-2 x-15} x4+5x33x5−75x3​⋅x2−2x−15x2+10x+21​\newlineAnswer:

Fully simplify the expression below and write your answer as a single fraction. $\newline$ $\frac{3 x^{5}-75 x^{3}}{x^{4}+5 x^{3}} \cdot \frac{x^{2}+10 x+21}{x^{2}-2 x-15}$ $\newline$ Answer: