AI tutor
Full solution
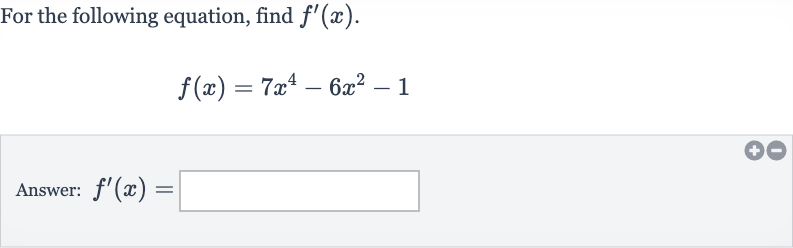
Q. For the following equation, find .Answer:
- Apply Power Rule: To find the derivative of the function , we will use the power rule for differentiation. The power rule states that the derivative of with respect to is .
- Derivative of : Apply the power rule to the first term . The derivative of with respect to is .
- Derivative of : Apply the power rule to the second term . The derivative of with respect to is .
- Derivative of constant: The third term is a constant, and the derivative of a constant is .
- Combine derivatives: Combine the derivatives of all terms to get the derivative of the entire function . This gives us .
- Simplify final derivative: Simplify the expression by removing the at the end, as it does not affect the value of the derivative. The final derivative is .
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help