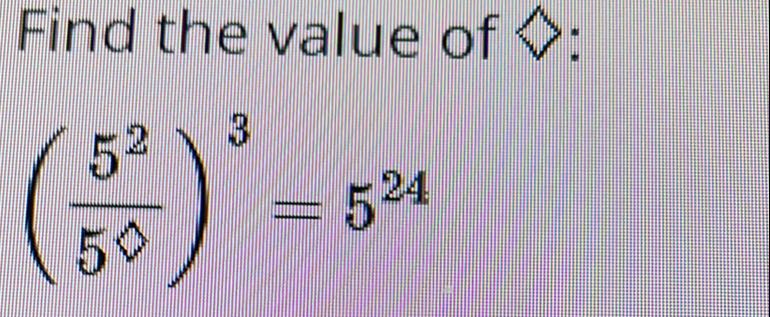AI tutor
Full solution
Q. Find the value of :
- Identify Equation & Property: Identify the given equation and the property of exponents that when dividing like bases, we subtract the exponents.The equation is .Using the property of exponents, we get .
- Apply Power to Exponent: Simplify the equation by applying the power to the exponent inside the parentheses..
- Set Exponents Equal: Since the bases are the same, we can set the exponents equal to each other. .
- Divide to Solve: Divide both sides of the equation by to solve for the variable "diamond".
- Isolate & Simplify: Simplify the equation to isolate the term with "diamond"..
- Add & Subtract to Solve: Add "diamond" to both sides and subtract from both sides to solve for "diamond".
- Calculate Final Value: Calculate the final value of "diamond"..
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help