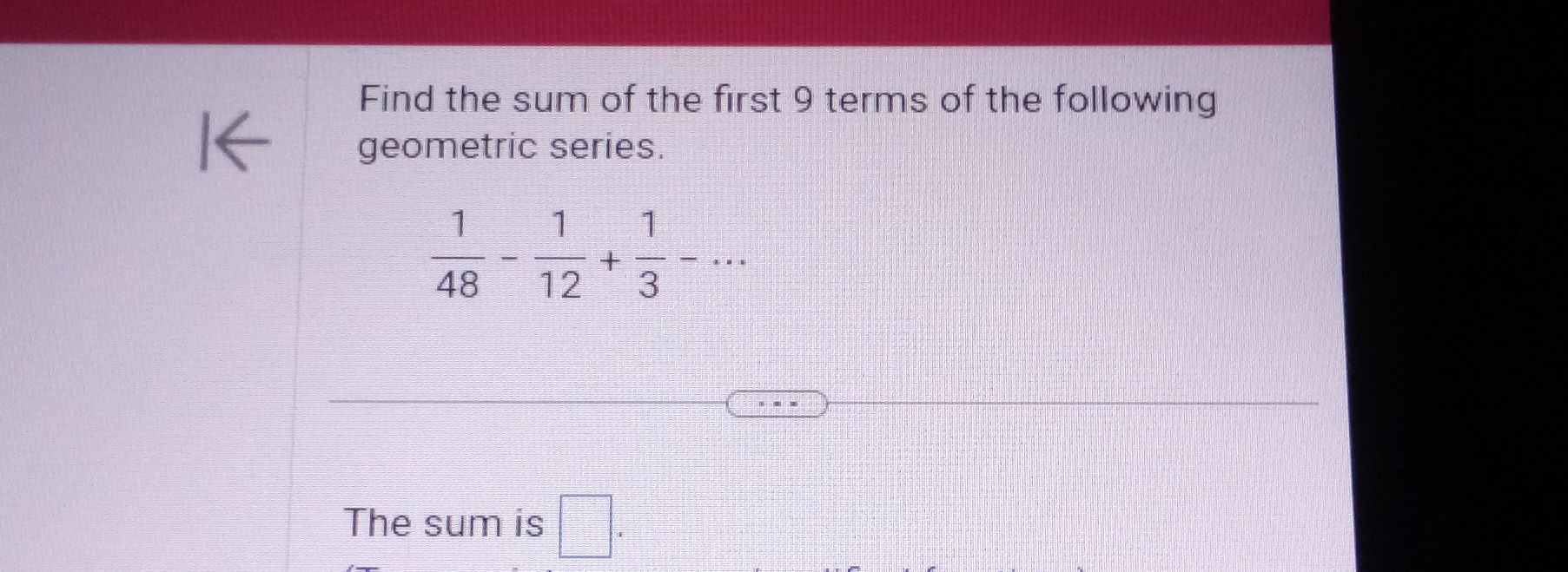
Find the sum of the first 9 terms of the following geometric series. (1)/(48)-(1)/(12)+(1)/(3)-dots The sum is ◻.

Question

Find the sum of the first 9 terms of the following geometric series.  (1)/(48)-(1)/(12)+(1)/(3)-dots The sum is ◻.

Bytelearn · Accepted Answer

Identify terms and ratio: Identify the first term (a) and the common ratio (r) of the geometric series. The first term a is (1/48). To find the common ratio r, divide the second term by the first term: r = (-1/12) / (1/48) = -4.Use sum formula: Use the formula for the sum of the first n terms of a geometric series: S_n = a(1 - r^n) / (1 - r), where n is the number of terms. Here, n = 9, a = 1/48, and r = -4.Calculate (-4)^9: Plug the values into the formula: S_9 = (1/48)(1 - (-4)^9) / (1 - (-4)).Substitute and simplify: Calculate (-4)^9. Since 4 is even and the exponent 9 is odd, the result will be negative: (-4)^9 = -262144.Add numbers in parentheses: Substitute the value into the sum formula: S_9 = (1/48)(1 - (-262144)) / (1 + 4).Substitute sum into formula: Simplify the expression: S_9 = (1/48)(1 + 262144) / 5.Multiply numerator: Add the numbers inside the parentheses: 1 + 262144 = 262145.Divide by denominator: Substitute the sum into the formula: S_9 = (1/48)(262145) / 5.Final sum: Multiply the numerator: (1/48) * 262145 = 5461.35416667 (rounded to 8 decimal places).Divide by the denominator: 5461.35416667 / 5 = 1092.27083333 (rounded to 8 decimal places).The sum of the first 9 terms of the geometric series is approximately 1092.27083333.

Find the sum of the first $9$ terms of the following geometric series. $\newline$ $\frac{1}{48}-\frac{1}{12}+\frac{1}{3}-\ldots$ $\newline$ The sum is $\square$ .

Full solution

More problems from Operations with rational exponents

Related topics

Find the sum of the first 999 terms of the following geometric series.\newline148−112+13−… \frac{1}{48}-\frac{1}{12}+\frac{1}{3}-\ldots 481​−121​+31​−…\newlineThe sum is □\square□.

Find the sum of the first $9$ terms of the following geometric series. $\newline$ $\frac{1}{48}-\frac{1}{12}+\frac{1}{3}-\ldots$ $\newline$ The sum is $\square$ .