Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the sum of the first 7 terms of the following series, to the nearest integer. 6,(9)/(2),(27)/(8),dots Answer:

Find the sum of the first 77 terms of the following series, to the nearest integer.\newline6,92,278,… 6, \frac{9}{2}, \frac{27}{8}, \ldots \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Operations with rational exponentsright chevron icon

Full solution

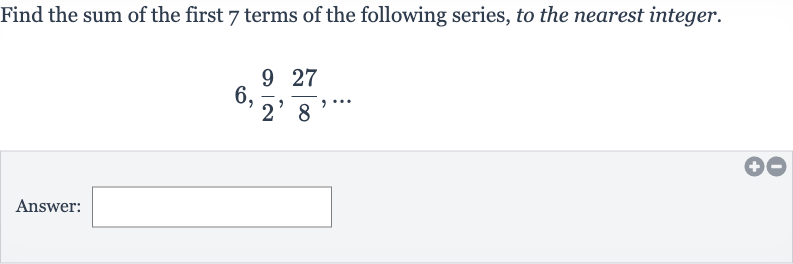
Q. Find the sum of the first 77 terms of the following series, to the nearest integer.\newline6,92,278,… 6, \frac{9}{2}, \frac{27}{8}, \ldots \newlineAnswer:
  1. Identify pattern: Identify the pattern of the series. The series starts with 66 and each subsequent term is multiplied by (3/2)(3/2) to get the next term. This is a geometric series with the first term a=6a = 6 and the common ratio r=(3/2)r = (3/2).
  2. Use formula for sum: Use the formula for the sum of the first nn terms of a geometric series, which is Sn=a(1−rn)/(1−r)S_n = a(1 - r^n) / (1 - r), where SnS_n is the sum of the first nn terms, aa is the first term, rr is the common ratio, and nn is the number of terms.
  3. Plug in values: Plug in the values for the first 77 terms: a=6a = 6, r=32r = \frac{3}{2}, and n=7n = 7. Calculate the sum S7=6(1−(32)7)/(1−32)S_7 = 6\left(1 - \left(\frac{3}{2}\right)^7\right) / \left(1 - \frac{3}{2}\right).
  4. Calculate (32)7(\frac{3}{2})^7: Calculate (32)7(\frac{3}{2})^7. This is 3727=2187128\frac{3^7}{2^7} = \frac{2187}{128}.
  5. Substitute in formula: Substitute the value of (32)7(\frac{3}{2})^7 into the sum formula: S7=6(1−2187128)/(1−32)S_7 = 6(1 - \frac{2187}{128}) / (1 - \frac{3}{2}).
  6. Simplify expression: Simplify the expression: S7=6(1−2187128)(−12).S_7 = \frac{6(1 - \frac{2187}{128})}{(-\frac{1}{2})}.
  7. Simplify numerator: Simplify the numerator: 1−2187128=(128128)−(2187128)=128−2187128=−2059128.1 - \frac{2187}{128} = \left(\frac{128}{128}\right) - \left(\frac{2187}{128}\right) = \frac{128 - 2187}{128} = -\frac{2059}{128}.
  8. Substitute numerator: Substitute the simplified numerator into the sum formula: S7=6(−2059/128)(−1/2)S_7 = \frac{6(-2059/128)}{(-1/2)}.
  9. Simplify denominator: Simplify the denominator: −12-\frac{1}{2} is the same as multiplying by −2-2. So, S7=6(−2059128)×−2S_7 = 6(-\frac{2059}{128}) \times -2.
  10. Multiply terms: Multiply the terms: S7=−12×(−2059/128)S_7 = -12 \times (-2059/128).
  11. Simplify multiplication: Simplify the multiplication: S7=24708128S_7 = \frac{24708}{128}.
  12. Divide for sum: Divide to find the sum to the nearest integer: S7≈24708128≈193S_7 \approx \frac{24708}{128} \approx 193.

More problems from Operations with rational exponents

Question
f(x)=6x+52−14+5x f(x)=\frac{6 x+5}{2-\sqrt{14+5 x}} \newlineWe want to find lim⁡x→−2f(x) \lim _{x \rightarrow-2} f(x) .\newlineWhat happens when we use direct substitution?\newlineChoose 11 answer:\newline(A) The limit exists, and we found it!\newline(B) The limit doesn't exist (probably an asymptote).\newline(C) The result is indeterminate.
Get tutor helpright-arrow

Posted 9 months ago

Question
Let x4+y2=17 x^{4}+y^{2}=17 .\newlineWhat is the value of d2ydx2 \frac{d^{2} y}{d x^{2}} at the point (−2,1) (-2,1) ?\newlineGive an exact number.
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the area of the region bound by the graphs of f(x)=x−2,g(x)=14−x f(x)=\sqrt{x-2}, g(x)=14-x , and x=2 x=2 ?\newlineChoose 11 answer:\newline(A) 196 \frac{19}{6} \newline(B) 992 \frac{99}{2} \newline(C) 1512 \frac{151}{2} \newline(D) 452 \frac{45}{2}
Get tutor helpright-arrow

Posted 7 months ago

Question
Let g(x)=x43 g(x)=x^{\frac{4}{3}} .\newlineg′(27)= g^{\prime}(27)=
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify ln⁡(1e) \ln \left(\frac{1}{\sqrt{e}}\right) \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify ln⁡(1e) \ln \left(\frac{1}{e}\right) \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
y=(sin⁡−1(5x2))3y=(\sin^{-1}(5x^{2}))^{3}
Get tutor helpright-arrow

Posted 8 months ago

Question
(10x3−5x2−6x)÷(2x2)\left(10x^{3}-5x^{2}-6x\right)\div\left(2x^{2}\right)
Get tutor helpright-arrow

Posted 8 months ago

Question
y=cos⁡4xsin⁡4xy=\cos^{4}x\sin^{4}x
Get tutor helpright-arrow

Posted 8 months ago

Question
35−310\frac{3}{5}-\frac{3}{10}
Get tutor helpright-arrow

Posted 8 months ago

View all (333)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant