Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the positive solution of the equation. 6x^((6)/(7))+23=24599 Answer:

Find the positive solution of the equation.\newline6x67+23=24599 6 x^{\frac{6}{7}}+23=24599 \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Operations with rational exponentsright chevron icon

Full solution

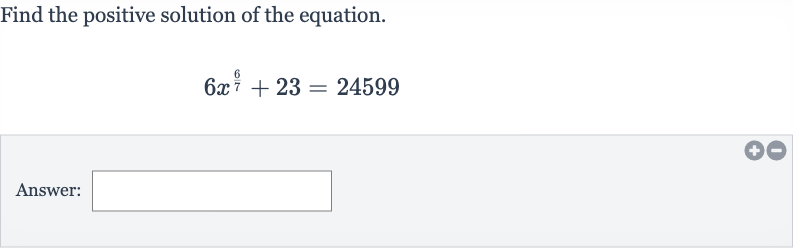
Q. Find the positive solution of the equation.\newline6x67+23=24599 6 x^{\frac{6}{7}}+23=24599 \newlineAnswer:
  1. Isolate variable term: First, we need to isolate the term with the variable xx on one side of the equation. To do this, we subtract 2323 from both sides of the equation.\newline6x(6/7)+23−23=24599−236x^{(6/7)} + 23 - 23 = 24599 - 23
  2. Simplify right side: Now, we simplify the right side of the equation by performing the subtraction.\newline6x67=24599−236x^{\frac{6}{7}} = 24599 - 23\newline6x67=245766x^{\frac{6}{7}} = 24576
  3. Divide by 66: Next, we divide both sides of the equation by 66 to solve for x(6/7)x^{(6/7)}. \newline6x(6/7)6=245766\frac{6x^{(6/7)}}{6} = \frac{24576}{6}\newlinex(6/7)=4096x^{(6/7)} = 4096
  4. Recognize power of 22: We recognize that 40964096 is a power of 22. Specifically, 40964096 is 22 raised to the 1212th power (2122^{12}).\newlinex67=212x^{\frac{6}{7}} = 2^{12}
  5. Raise to reciprocal power: To solve for xx, we need to raise both sides of the equation to the reciprocal of 67\frac{6}{7}, which is 76\frac{7}{6}.(x67)76=(212)76(x^{\frac{6}{7}})^{\frac{7}{6}} = (2^{12})^{\frac{7}{6}}
  6. Multiply exponents: When we raise a power to a power, we multiply the exponents. On the left side, (67)×(76)(\frac{6}{7}) \times (\frac{7}{6}) equals 11, so we are left with xx. On the right side, we multiply the exponents 1212 and (76)(\frac{7}{6}).x=212×76x = 2^{12 \times \frac{7}{6}}
  7. Simplify exponent: Now we simplify the exponent on the right side by multiplying 1212 and (7/6)(7/6). \newlinex=284/6x = 2^{84/6}\newlinex=214x = 2^{14}
  8. Calculate final value: Finally, we calculate 2142^{14} to find the value of xx.\newlinex=16384x = 16384

More problems from Operations with rational exponents

Question
f(x)=6x+52−14+5x f(x)=\frac{6 x+5}{2-\sqrt{14+5 x}} \newlineWe want to find lim⁡x→−2f(x) \lim _{x \rightarrow-2} f(x) .\newlineWhat happens when we use direct substitution?\newlineChoose 11 answer:\newline(A) The limit exists, and we found it!\newline(B) The limit doesn't exist (probably an asymptote).\newline(C) The result is indeterminate.
Get tutor helpright-arrow

Posted 9 months ago

Question
Let x4+y2=17 x^{4}+y^{2}=17 .\newlineWhat is the value of d2ydx2 \frac{d^{2} y}{d x^{2}} at the point (−2,1) (-2,1) ?\newlineGive an exact number.
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the area of the region bound by the graphs of f(x)=x−2,g(x)=14−x f(x)=\sqrt{x-2}, g(x)=14-x , and x=2 x=2 ?\newlineChoose 11 answer:\newline(A) 196 \frac{19}{6} \newline(B) 992 \frac{99}{2} \newline(C) 1512 \frac{151}{2} \newline(D) 452 \frac{45}{2}
Get tutor helpright-arrow

Posted 7 months ago

Question
Let g(x)=x43 g(x)=x^{\frac{4}{3}} .\newlineg′(27)= g^{\prime}(27)=
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify ln⁡(1e) \ln \left(\frac{1}{\sqrt{e}}\right) \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify ln⁡(1e) \ln \left(\frac{1}{e}\right) \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
y=(sin⁡−1(5x2))3y=(\sin^{-1}(5x^{2}))^{3}
Get tutor helpright-arrow

Posted 8 months ago

Question
(10x3−5x2−6x)÷(2x2)\left(10x^{3}-5x^{2}-6x\right)\div\left(2x^{2}\right)
Get tutor helpright-arrow

Posted 8 months ago

Question
y=cos⁡4xsin⁡4xy=\cos^{4}x\sin^{4}x
Get tutor helpright-arrow

Posted 8 months ago

Question
35−310\frac{3}{5}-\frac{3}{10}
Get tutor helpright-arrow

Posted 8 months ago

View all (333)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant