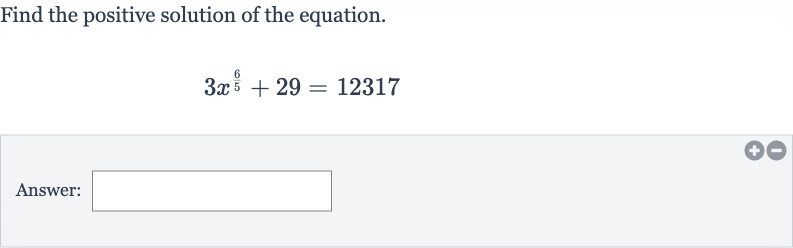Full solution
Q. Find the positive solution of the equation.Answer:
- Isolate variable term: Isolate the term with the variable.Subtract from both sides of the equation to isolate the term with the variable .
- Subtract : Divide both sides by to solve for .
- Divide by : Recognize that is a power of . is raised to the th power, since .
- Recognize power of : Take the root of both sides to solve for .
- Take th root: Simplify the exponent on the right side.
- Simplify exponent: Calculate .\)\)
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help