Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find
lim_(x rarr3)((x-5)^(2))/((x-3)^(2)).
Choose 1 answer:
(A)
-(2)/(3)
(B) 0
(C)
(11)/(3)
(D) The limit doesn't exist

Find $\lim _{x \rightarrow 3} \frac{(x-5)^{2}}{(x-3)^{2}}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $-\frac{2}{3}$ $\newline$ (B) $0$ $\newline$ (C) $\frac{11}{3}$ $\newline$ D D The limit doesn't exist

View step-by-step help

View step-by-step help

Compare linear and exponential growth

Full solution

Q. Find

\lim _{x \rightarrow 3} \frac{(x-5)^{2}}{(x-3)^{2}}

.

\newline

Choose

1

answer:

\newline

(A)

-\frac{2}{3}

\newline

(B)

0

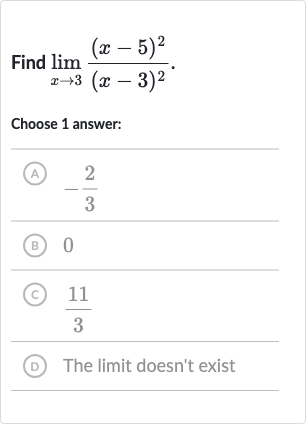
\newline

(C)

\frac{11}{3}

\newline

D D The limit doesn't exist

Identify the form: Identify the form of the limit. $\newline$ We are asked to find the limit of the function $(x-5)^2 / (x-3)^2$ as $x$ approaches $3$ . Let's plug in $x = 3$ to see what form the limit takes. $\newline$ $\lim_{x \to 3}\frac{(x-5)^2}{(x-3)^2} = \frac{(3-5)^2}{(3-3)^2} = (-2)^2 / (0)^2.$ $\newline$ We notice that the denominator becomes $0$ , which suggests that the limit might be of the form $0/0$ , indicating a possible indeterminate form.
Simplify the expression: Simplify the expression if possible. $\newline$ Since we have an indeterminate form, we can try to simplify the expression or use L'Hôpital's Rule. However, in this case, the expression is already in its simplest form, and L'Hôpital's Rule is not necessary because we can directly evaluate the limit by canceling out the common factors.
Factor and cancel: Factor and cancel if possible. $\newline$ We notice that the numerator and the denominator are both perfect squares. Let's factor them out: $\newline$ $\lim_{x \to 3}\frac{(x-5)^2}{(x-3)^2} = \lim_{x \to 3}\left(\frac{x-5}{x-3}\right)^2$ . $\newline$ Now, we can see that the $\frac{x-5}{x-3}$ term will not be zero when x approaches $3$ , so we can evaluate the limit by plugging in $x = 3$ : $\newline$ $\lim_{x \to 3}\left(\frac{x-5}{x-3}\right)^2 = \left(\frac{3-5}{3-3}\right)^2 = \left(\frac{-2}{0}\right)^2$ . $\newline$ However, we made a mistake here. We cannot divide by zero, and the term $(x-3)$ in the denominator will indeed be zero when $x = 3$ , which means we cannot simply plug in the value of $x = 3$ .

More problems from Compare linear and exponential growth

Question

Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits

x

days to pick up the motorcycle.

\newline

Write an equation for the function. If it is linear, write it in the form

g(x) = mx + b

. If it is exponential, write it in the form

g(x) = a(b)^x

\newline

g(x) = \underline{\hspace{3em}}

Posted 5 months ago

Question

f(t)=-2t-7

change over the interval from

t=-7

t=-6

\newline

\newline

\left[\text{f(t) decreases by } 2\right]

\newline

\left[\text{f(t) increases by } 2\right]

\newline

\left[\text{f(t) increases by } 200\%\right]

\newline

\left[\text{f(t) decreases by a factor of } 2\right]

Posted 5 months ago

Question

g(t)=9^t

change over the interval from

t=1

t=3

\newline

\newline

\left[\text{g(t) decreases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by } 18\%\right]

\newline

\left[\text{g(t) decreases by } 9\%\right]

Posted 5 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A)f(x) = 8x + 3.3

\newline

(B)g(x) = 3.3^x - 5

Posted 6 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A) \ f(x) = 2x + 9

\newline

(B)\ g(x) = 2^x

Posted 6 months ago

Question

f(x)

g(x)

are differentiable.

\newline

h(x)

h(x)=\frac{g(x)}{f(x)}

\newline

f(8)=1

f'(8)=-6

g(8)=8

g'(8)=-10

h'(8)

\newline

Simplify any fractions.

\newline

h'(8)=

Posted 6 months ago

Question

p(x)

q(x)

are differentiable.

\newline

r(x)

r(x)= \frac{p(x)}{q(x)}

\newline

p(3)= 2

p'(3)= 4

q(3)= 6

q'(3)= 9

r'(3)

\newline

Simplify any fractions.

\newline

r'(3)=

Posted 7 months ago

Question

u(x)

v(x)

are differentiable.

\newline

w(x)

w(x)= \frac{u(x)}{v(x)}

\newline

u(5)= 3

u'(5)= -2

v(5)= 7

v'(5)= 1

w'(5)

\newline

Simplify any fractions.

\newline

w'(5)=

Posted 7 months ago

Question

a(x)

b(x)

are differentiable.

\newline

c(x)

c(x)= \frac{a(x)}{b(x)}

\newline

a(2)= 4

a'(2)= 5

b(2)= 1

b'(2)= -3

c'(2)

\newline

Simplify any fractions.

\newline

c'(2)=

Posted 7 months ago

Question

m(x)

n(x)

are differentiable.

\newline

o(x)

o(x)= \frac{m(x)}{n(x)}

\newline

m(7)= 2

m'(7)= -1

n(7)= 4

n'(7)= 8

o'(7)

\newline

Simplify any fractions.

\newline

o'(7)=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant