Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find
lim_(x rarr oo)(x^(2)-4)/(x+4).
Choose 1 answer:
(A) 1
(B) -1
(C) 0
(D) The limit is unbounded

Find $\lim _{x \rightarrow \infty} \frac{x^{2}-4}{x+4}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $1$ $\newline$ (B) $-1$ $\newline$ (C) $0$ $\newline$ (D) The limit is unbounded

View step-by-step help

View step-by-step help

Find limits of polynomials and rational functions

Full solution

Q. Find

\lim _{x \rightarrow \infty} \frac{x^{2}-4}{x+4}

.

\newline

Choose

1

answer:

\newline

(A)

1

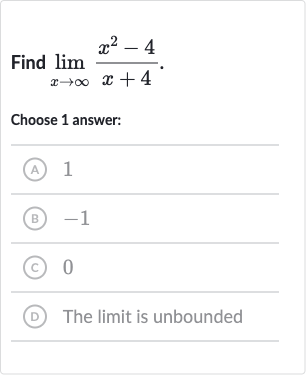
\newline

(B)

-1

\newline

(C)

0

\newline

(D) The limit is unbounded

Analyze degrees of polynomials: To find the limit of the given function as $x$ approaches infinity, we can analyze the degrees of the polynomials in the numerator and the denominator. $\newline$ The degree of the polynomial in the numerator ( $x^2 - 4$ ) is $2$ . $\newline$ The degree of the polynomial in the denominator ( $x + 4$ ) is $1$ . $\newline$ Since the degree of the numerator is higher than the degree of the denominator, we can expect the limit to be unbounded.
Divide terms to simplify expression: To confirm our expectation, we can divide each term in the numerator by $x$ , the highest power of $x$ in the denominator, to simplify the expression. $\newline$ This gives us $(\frac{x^2}{x} - \frac{4}{x}) / (\frac{x}{x} + \frac{4}{x})$ . $\newline$ Simplifying this, we get $(x - \frac{4}{x}) / (1 + \frac{4}{x})$ .
Simplify expression: As $x$ approaches infinity, the terms $\frac{4}{x}$ in the numerator and $\frac{4}{x}$ in the denominator approach $0$ . So the expression simplifies to $\frac{x}{1}$ , which is just $x$ .
Approach of terms as $x$ approaches infinity: Since $x$ approaches infinity, the limit of the function as $x$ approaches infinity is also infinity. $\newline$ Therefore, the limit is unbounded.

More problems from Find limits of polynomials and rational functions

Question

f(x)=\frac{6 x^{3}}{3 x+2}

\newline

\lim _{x \rightarrow \infty} f(x)

\newline

1

\newline

2

\newline

3

\newline

0

\newline

(D) The limit is unbounded

Posted 3 months ago

Question

\lim _{x \rightarrow 4} \frac{3 x}{(x-2)(x+2)}

\newline

1

\newline

\frac{1}{4}

\newline

\frac{3}{4}

\newline

1

\newline

(D) The limit doesn't exist

Posted 2 months ago

Question

What is the average value of

x^{3}-9 x

on the interval

-1 \leq x \leq 3

Posted 1 month ago

Question

What happens to the value of the expression

\frac{3y}{2y}

y

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 2 months ago

Question

x+7

is a factor of the polynomial function

g

, what is the value of

g(7)

Posted 2 months ago

Question

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE).

\newline

\lim _{x \rightarrow \infty} \frac{\sqrt{23 x+64 x^{9}}}{7 x^{4}+6 x^{3}}

\newline

Posted 2 months ago

Question

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE).

\newline

\lim _{x \rightarrow \infty} \frac{\sqrt{25 x^{4}-28 x^{2}}}{3 x+5 x^{2}}

\newline

Posted 2 months ago

Question

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE).

\newline

\lim _{x \rightarrow \infty} \frac{\sqrt{-19 x^{3}+36 x^{4}}}{3+x+x^{2}}

\newline

Posted 2 months ago

Question

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE).

\newline

\lim _{x \rightarrow \infty} \frac{\sqrt{-3 x+x^{4}}}{7+8 x^{2}+10 x}

\newline

Posted 2 months ago

Question

Aditya's dog routinely eats Aditya's leftovers, which vary seasonally. As a result, his weight fluctuates throughout the year.

\newline

The dog's weight

W(t)

\mathrm{kg}

) as a function of time

t

(in days) over the course of a year can be modeled by a sinusoidal expression of the form

a \cdot \cos (b \cdot t)+d

\newline

t=0

, the start of the year, he is at his maximum weight of

9.1 \mathrm{~kg}

. One-quarter of the year later, when

t=91.25

, he is at his average weight of

8.2 \mathrm{~kg}

\newline

W(t)

\newline

t

should be in radians.

Posted 21 hours ago