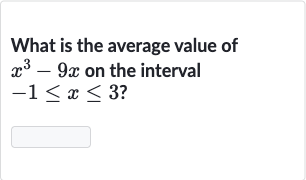Full solution

Q. What is the average value of

x^{3}-9 x

on the interval

-1 \leq x \leq 3

Set up integral: To find the average value of the function $x^3 - 9x$ on the interval from $-1$ to $3$ , we need to integrate the function over the interval and then divide by the length of the interval.
Find antiderivative: First, we set up the integral of the function $x^3 - 9x$ from $-1$ to $3$ . Integral from $-1$ to $3$ of $(x^3 - 9x) \, dx$
Evaluate antiderivative: Next, we find the antiderivative of $x^3 - 9x$ . The antiderivative of $x^3$ is $(1/4)x^4$ , and the antiderivative of $-9x$ is $(-9/2)x^2$ . So, the antiderivative of $x^3 - 9x$ is $(1/4)x^4 - (9/2)x^2$ .
Calculate interval length: We evaluate the antiderivative from $-1$ to $3$ .
$\left[\frac{1}{4}x^4 - \frac{9}{2}x^2\right]$ evaluated from $-1$ to $3$
= $\left[\frac{1}{4}(3)^4 - \frac{9}{2}(3)^2\right] - \left[\frac{1}{4}(-1)^4 - \frac{9}{2}(-1)^2\right]$
= $\left[\frac{1}{4}(81) - \frac{9}{2}(9)\right] - \left[\frac{1}{4}(1) - \frac{9}{2}(1)\right]$
= $\left[\frac{81}{4} - \frac{81}{2}\right] - \left[\frac{1}{4} - \frac{9}{2}\right]$
= $[20.25 - 40.5] - [0.25 - 4.5]$
= $-20.25 + 4.25$
= $3$ $0$
Divide for average value: Now, we calculate the length of the interval from $-1$ to $3$ . $\newline$ Length of the interval = $3 - (-1) = 3 + 1 = 4$
Divide for average value: Now, we calculate the length of the interval from $-1$ to $3$ . Length of the interval = $3 - (-1) = 3 + 1 = 4$ Finally, we divide the result of the integral by the length of the interval to find the average value. Average value = Integral result / Length of the interval Average value = $-16 / 4$ Average value = $-4$