Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find lim_(h rarr0)(6sqrt(9+h)-6sqrt9)/(h). Choose 1 answer: (A) 1 (B) 6 (C) 18 (D) The limit doesn't exist

Find lim⁡h→069+h−69h \lim _{h \rightarrow 0} \frac{6 \sqrt{9+h}-6 \sqrt{9}}{h} .\newlineChoose 11 answer:\newline(A) 11\newline(B) 66\newline(C) 1818\newline(D) The limit doesn't exist

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Solve quadratic inequalitiesright chevron icon

Full solution

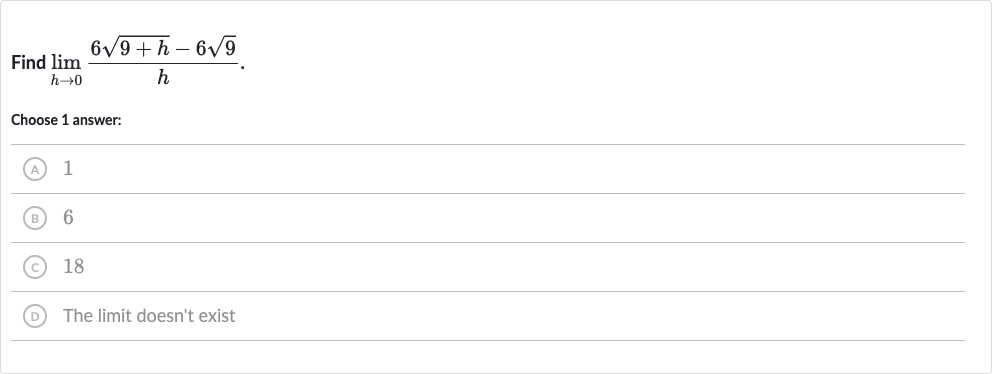
Q. Find lim⁡h→069+h−69h \lim _{h \rightarrow 0} \frac{6 \sqrt{9+h}-6 \sqrt{9}}{h} .\newlineChoose 11 answer:\newline(A) 11\newline(B) 66\newline(C) 1818\newline(D) The limit doesn't exist
  1. Identify Problem: Identify the limit problem and apply the conjugate to simplify the expression.\newlineMultiply the numerator and denominator by the conjugate of the numerator: 69+h+69.6\sqrt{9+h}+6\sqrt{9}.
  2. Apply Conjugate: Perform the multiplication in the numerator: (69+h−69)(69+h+69)(6\sqrt{9+h}-6\sqrt{9})(6\sqrt{9+h}+6\sqrt{9}).
  3. Multiply Numerator and Denominator: Use the difference of squares formula: a2−b2=(a−b)(a+b)a^2 - b^2 = (a - b)(a + b). The numerator becomes: 36(9+h)−36×936(9+h) - 36\times 9.
  4. Use Difference of Squares: Simplify the numerator: 36×9+36h−36×936\times 9 + 36h - 36\times 9.
  5. Simplify Numerator: Cancel out 36×936\times 9 terms in the numerator to get 36h36h.
  6. Cancel Terms: The expression simplifies to 36h/h36h/h.
  7. Final Simplification: Cancel out the hh terms to get 3636.

More problems from Solve quadratic inequalities

Question
The Smiths and the Johnsons were competing in the final leg of the Amazing Race. In their race to the finish, the Smiths immediately took off on a 165165 kilometer path traveling at an average speed of v v kilometers per hour.\newlineThe Johnsons' start was delayed by 12 \frac{1}{2} hour. Eventually, they took a 180180 kilometer path to the finish, traveling at an average speed that was 2020 kilometers per hour faster than the Smiths' speed.\newlineThe Johnsons arrived at the finish line first and won the race!\newlineWrite an inequality in terms of v v that models the situation.
Get tutor helpright-arrow

Posted 3 months ago

Question
−10x−3≥8x+4 -10 x-3 \geq 8 x+4 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newlineA) x≤−718 x \leq-\frac{7}{18} \newline(B) x≤−72 x \leq-\frac{7}{2} \newline(C) x≤−118 x \leq-\frac{1}{18} \newline(D) x≥−718 x \geq-\frac{7}{18}
Get tutor helpright-arrow

Posted 3 months ago

Question
−12x<−72 -12 x<-72 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<6 x<6 \newline(B) x>6 x>6 \newline(C) x<16 x<\frac{1}{6} \newline(D) x>16 x>\frac{1}{6}
Get tutor helpright-arrow

Posted 3 months ago

Question
8x+6<4x+10 8 x+6<4 x+10 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<13 x<\frac{1}{3} \newline(B) x<4 x<4 \newline(C) x<1 x<1 \newline(D) x>1 x>1
Get tutor helpright-arrow

Posted 3 months ago

Question
6x−2<2x+3 6 x-2<2 x+3 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<54 x<\frac{5}{4} \newline(B) x>54 x>\frac{5}{4} \newline(C) x<14 x<\frac{1}{4} \newline(D) x<58 x<\frac{5}{8}
Get tutor helpright-arrow

Posted 3 months ago

Question
16<−4x 16<-4 x \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<−4 x<-4 \newline(B) x>−4 x>-4 \newline(C) x<−14 x<-\frac{1}{4} \newline(D) x>−14 x>-\frac{1}{4}
Get tutor helpright-arrow

Posted 3 months ago

Question
−2>3(b+4)−2 -2>\frac{3(b+4)}{-2} \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) b<−3 b<-3 \newline(B) b<−163 b<-\frac{16}{3} \newline(C) b>−83 b>-\frac{8}{3} \newline(D) b>0 b>0
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→42−4x−12x−4 \lim _{x \rightarrow 4} \frac{2-\sqrt{4 x-12}}{x-4} .\newlineChoose 11 answer:\newline(A) 22\newline(B) 11\newline(C) −1-1\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→2x4−4x3+4x2x−2 \lim _{x \rightarrow 2} \frac{x^{4}-4 x^{3}+4 x^{2}}{x-2} .\newlineChoose 11 answer:\newline(A) −4-4\newline(B) 00\newline(C) 44\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Let f f be a continuous function on the closed interval [−5,0] [-5,0] , where f(−5)=0 f(-5)=0 and f(0)=5 f(0)=5 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) f(c)=−2 f(c)=-2 for at least one c c between 00 and 55\newline(B) f(c)=2 f(c)=2 for at least one c c between 00 and 55\newline(C) f(c)=−2 f(c)=-2 for at least one c c between −5-5 and 00\newline(D) f(c)=2 f(c)=2 for at least one c c between −5-5 and 00
Get tutor helpright-arrow

Posted 3 months ago

View all (28)