Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find lim_(h rarr0)(6arctan(1+h)-6arctan(1))/(h). Choose 1 answer: (A) 1 (B) 3 (C) 6 (D) The limit doesn't exist

Find lim⁡h→06arctan⁡(1+h)−6arctan⁡(1)h \lim _{h \rightarrow 0} \frac{6 \arctan (1+h)-6 \arctan (1)}{h} .\newlineChoose 11 answer:\newline(A) 11\newline(B) 33\newline(C) 66\newline(D) The limit doesn't exist

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Solve quadratic inequalitiesright chevron icon

Full solution

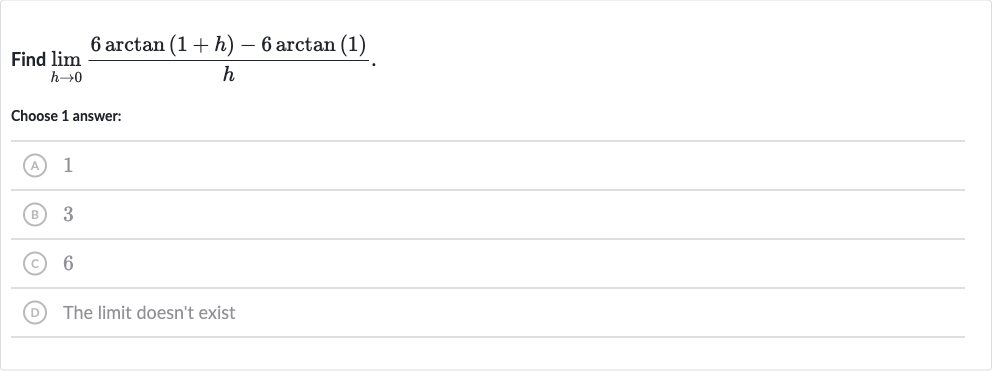
Q. Find lim⁡h→06arctan⁡(1+h)−6arctan⁡(1)h \lim _{h \rightarrow 0} \frac{6 \arctan (1+h)-6 \arctan (1)}{h} .\newlineChoose 11 answer:\newline(A) 11\newline(B) 33\newline(C) 66\newline(D) The limit doesn't exist
  1. Identify Limit: Identify the limit to solve. lim⁡h→06arctan⁡(1+h)−6arctan⁡(1)h\lim_{h \rightarrow 0}\frac{6\arctan(1+h)-6\arctan(1)}{h}
  2. Simplify with arctan⁡(1)\arctan(1): Use the fact that arctan⁡(1)=π4\arctan(1) = \frac{\pi}{4} to simplify the expression.lim⁡h→06arctan⁡(1+h)−6(π4)h\lim_{h \rightarrow 0}\frac{6\arctan(1+h)-6\left(\frac{\pi}{4}\right)}{h}
  3. Apply Limit to Terms: Apply the limit to the arctan⁡(1+h)\arctan(1+h) term.lim⁡h→06arctan⁡(1+h)h−lim⁡h→06(π/4)h\lim_{h \to 0}\frac{6\arctan(1+h)}{h} - \lim_{h \to 0}\frac{6(\pi/4)}{h}
  4. Simplify Constant Term: Simplify the second term, as 6(π/4)6(\pi/4) is a constant and its limit as hh approaches 00 is 00. \newlinelim⁡h→06arctan⁡(1+h)h−0\lim_{h \to 0}\frac{6\arctan(1+h)}{h} - 0
  5. Apply L'Hôpital's Rule: Apply L'Hôpital's Rule to the first term since it's in the indeterminate form 0/00/0. \newlinelim⁡h→0(6ddh(arctan⁡(1+h)))\lim_{h \to 0}(6\frac{d}{dh}(\arctan(1+h)))
  6. Differentiate arctan(1+h)\text{arctan}(1+h): Differentiate arctan(1+h)\text{arctan}(1+h) with respect to hh.ddh(arctan(1+h))=11+(1+h)2\frac{d}{dh}(\text{arctan}(1+h)) = \frac{1}{1+(1+h)^2}
  7. Substitute Derivative: Substitute the derivative back into the limit. lim⁡h→0(61+(1+h)2)\lim_{h \to 0}\left(\frac{6}{1+(1+h)^2}\right)
  8. Evaluate Limit: Evaluate the limit by plugging in h=0h = 0.61+(1+0)2=61+12=62=3\frac{6}{1+(1+0)^2} = \frac{6}{1+1^2} = \frac{6}{2} = 3

More problems from Solve quadratic inequalities

Question
The Smiths and the Johnsons were competing in the final leg of the Amazing Race. In their race to the finish, the Smiths immediately took off on a 165165 kilometer path traveling at an average speed of v v kilometers per hour.\newlineThe Johnsons' start was delayed by 12 \frac{1}{2} hour. Eventually, they took a 180180 kilometer path to the finish, traveling at an average speed that was 2020 kilometers per hour faster than the Smiths' speed.\newlineThe Johnsons arrived at the finish line first and won the race!\newlineWrite an inequality in terms of v v that models the situation.
Get tutor helpright-arrow

Posted 4 months ago

Question
−10x−3≥8x+4 -10 x-3 \geq 8 x+4 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newlineA) x≤−718 x \leq-\frac{7}{18} \newline(B) x≤−72 x \leq-\frac{7}{2} \newline(C) x≤−118 x \leq-\frac{1}{18} \newline(D) x≥−718 x \geq-\frac{7}{18}
Get tutor helpright-arrow

Posted 4 months ago

Question
−12x<−72 -12 x<-72 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<6 x<6 \newline(B) x>6 x>6 \newline(C) x<16 x<\frac{1}{6} \newline(D) x>16 x>\frac{1}{6}
Get tutor helpright-arrow

Posted 4 months ago

Question
8x+6<4x+10 8 x+6<4 x+10 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<13 x<\frac{1}{3} \newline(B) x<4 x<4 \newline(C) x<1 x<1 \newline(D) x>1 x>1
Get tutor helpright-arrow

Posted 4 months ago

Question
6x−2<2x+3 6 x-2<2 x+3 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<54 x<\frac{5}{4} \newline(B) x>54 x>\frac{5}{4} \newline(C) x<14 x<\frac{1}{4} \newline(D) x<58 x<\frac{5}{8}
Get tutor helpright-arrow

Posted 4 months ago

Question
16<−4x 16<-4 x \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x<−4 x<-4 \newline(B) x>−4 x>-4 \newline(C) x<−14 x<-\frac{1}{4} \newline(D) x>−14 x>-\frac{1}{4}
Get tutor helpright-arrow

Posted 4 months ago

Question
−2>3(b+4)−2 -2>\frac{3(b+4)}{-2} \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) b<−3 b<-3 \newline(B) b<−163 b<-\frac{16}{3} \newline(C) b>−83 b>-\frac{8}{3} \newline(D) b>0 b>0
Get tutor helpright-arrow

Posted 4 months ago

Question
Find lim⁡x→42−4x−12x−4 \lim _{x \rightarrow 4} \frac{2-\sqrt{4 x-12}}{x-4} .\newlineChoose 11 answer:\newline(A) 22\newline(B) 11\newline(C) −1-1\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Find lim⁡x→2x4−4x3+4x2x−2 \lim _{x \rightarrow 2} \frac{x^{4}-4 x^{3}+4 x^{2}}{x-2} .\newlineChoose 11 answer:\newline(A) −4-4\newline(B) 00\newline(C) 44\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 3 months ago

Question
Let f f be a continuous function on the closed interval [−5,0] [-5,0] , where f(−5)=0 f(-5)=0 and f(0)=5 f(0)=5 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) f(c)=−2 f(c)=-2 for at least one c c between 00 and 55\newline(B) f(c)=2 f(c)=2 for at least one c c between 00 and 55\newline(C) f(c)=−2 f(c)=-2 for at least one c c between −5-5 and 00\newline(D) f(c)=2 f(c)=2 for at least one c c between −5-5 and 00
Get tutor helpright-arrow

Posted 3 months ago

View all (28)