Find $\lim _{h \rightarrow 0} \frac{2 \sqrt[3]{8+h}-2 \sqrt[3]{8}}{h}$ $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{1}{12}$ $\newline$ (B) $\frac{1}{6}$ $\newline$ (C) $4$ $\newline$ (D) The limit doesn't exist

View step-by-step help

Home

Math Problems

Calculus

Euler's method

Full solution

Q. Find

\lim _{h \rightarrow 0} \frac{2 \sqrt[3]{8+h}-2 \sqrt[3]{8}}{h}

\newline

Choose

1

answer:

\newline

(A)

\frac{1}{12}

\newline

(B)

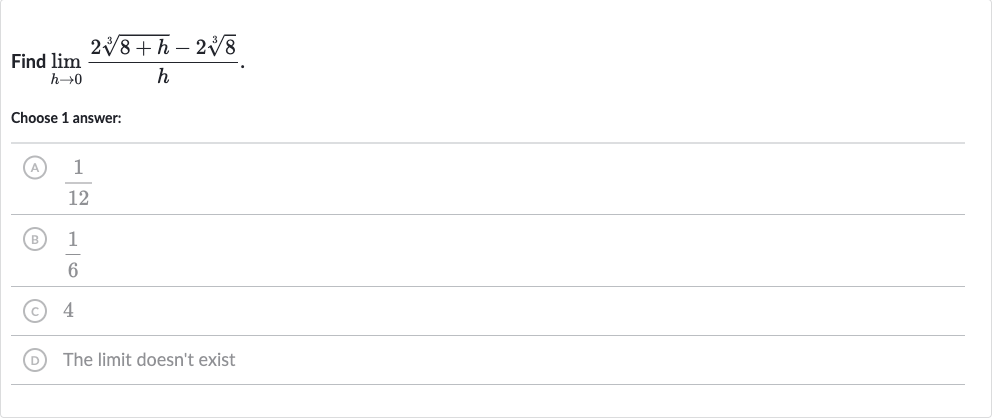
\frac{1}{6}

\newline

(C)

4

\newline

(D) The limit doesn't exist

Recognize Problem Type: First, let's recognize that this is a limit problem involving a difference quotient, which is a common way to find the derivative of a function at a point. We're essentially finding the derivative of $2\sqrt[3]{x}$ at $x=8$ .
Apply Definition of Derivative: To solve this, we can use the definition of the derivative, which is the limit of the difference quotient as $h$ approaches $0$ . So we're looking for $\lim_{h\to 0}\frac{2\sqrt[3]{8+h}-2\sqrt[3]{8}}{h}$ .
Apply L'Hôpital's Rule: We can apply L'Hôpital's Rule since the limit is in the indeterminate form $0/0$ . To do this, we need to differentiate the numerator and the denominator with respect to $h$ .
Differentiate Numerator: The derivative of the numerator with respect to $h$ is the derivative of $2\sqrt[3]{8+h}$ which is $(2/3)(8+h)^{(-2/3)}$ using the chain rule.
Differentiate Denominator: The derivative of the denominator with respect to $h$ is just $1$ since the derivative of $h$ with respect to $h$ is $1$ .
Apply L'Hôpital's Rule Again: Now we can apply L'Hôpital's Rule and take the limit of the derivatives: $\lim_{h\to 0}(\frac{2}{3})(8+h)^{-\frac{2}{3}}/1$ .
Plug in $h=0$ : Plugging $h=0$ into the derivative of the numerator, we get $(\frac{2}{3})(8)^{(-\frac{2}{3})}$ .
Simplify Result: Simplifying, $(\frac{2}{3})(8)^{-\frac{2}{3}}$ is $(\frac{2}{3})(\frac{1}{4})$ because $8^{-\frac{2}{3}}$ is the reciprocal of $8^{\frac{2}{3}}$ , which is $4$ .
Simplify Result: Simplifying, $(\frac{2}{3})(8)^{-\frac{2}{3}}$ is $(\frac{2}{3})(\frac{1}{4})$ because $8^{-\frac{2}{3}}$ is the reciprocal of $8^{\frac{2}{3}}$ , which is $4$ .Multiplying $(\frac{2}{3})$ by $(\frac{1}{4})$ gives us $(\frac{2}{3})\cdot(\frac{1}{4}) = \frac{1}{6}$ .