Full solution
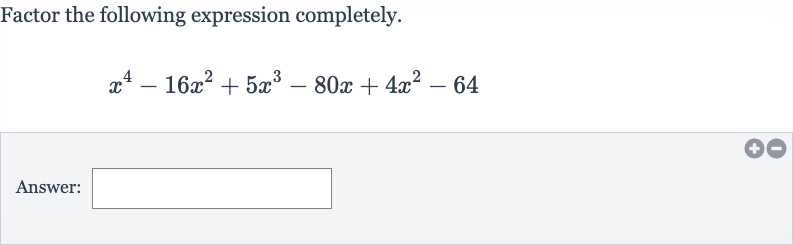
Q. Factor the following expression completely.Answer:
- Reorder and Combine Terms: First, we should reorder the terms of the expression by descending powers of to make it easier to factor.Now, combine like terms.
- Group and Separate Terms: Next, we look for common factors in groups of terms. We can group the first three terms and the last two terms separately. -
- Factor by Grouping: Now, factor by grouping. For the first group, we can factor out an . For the second group, we can factor out a .
- Factor Quadratic: We now factor the quadratic . This can be factored into .
- Final Factorization: We notice that there is no common factor between the two groups, so we cannot factor further. Therefore, the expression is completely factored.
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help