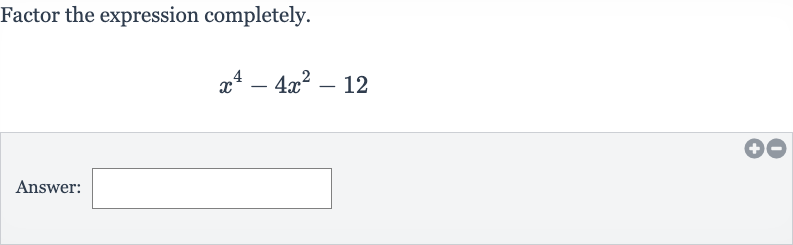
Factor the expression completely. x^(4)-4x^(2)-12 Answer:

Question

Factor the expression completely.  x^(4)-4x^(2)-12 Answer:

Bytelearn · Accepted Answer

Recognize Structure: Recognize the structure of the expression. The expression x^4 - 4x^2 - 12 resembles a quadratic in form, where x^2 is the variable instead of x. This suggests we can factor it similarly to how we would factor a quadratic equation.Factor as Quadratic: Factor the expression as if it were a quadratic. We are looking for two numbers that multiply to -12 and add up to -4 (the coefficient of the middle term). These numbers are -6 and +2. So, we can write the expression as (x^2 - 6)(x^2 + 2).Check for Further Factoring: Check for further factoring possibilities. The term (x^2 + 2) cannot be factored further over the real numbers because it does not have real roots. However, the term (x^2 - 6) is a difference of squares and can be factored further.Factor Difference of Squares: Factor the difference of squares. The expression x^2 - 6 can be written as (x - √6)(x + √6) because (x - √6)(x + √6) = x^2 - (√6)^2 = x^2 - 6.Combine Factors: Combine all factors to write the final factored expression. The completely factored form of the expression is (x - √6)(x + √6)(x^2 + 2).

Factor the expression completely. $\newline$ $x^{4}-4 x^{2}-12$ $\newline$ Answer:

Full solution

More problems from Operations with rational exponents

Related topics

Factor the expression completely.\newlinex4−4x2−12 x^{4}-4 x^{2}-12 x4−4x2−12\newlineAnswer:

Factor the expression completely. $\newline$ $x^{4}-4 x^{2}-12$ $\newline$ Answer: