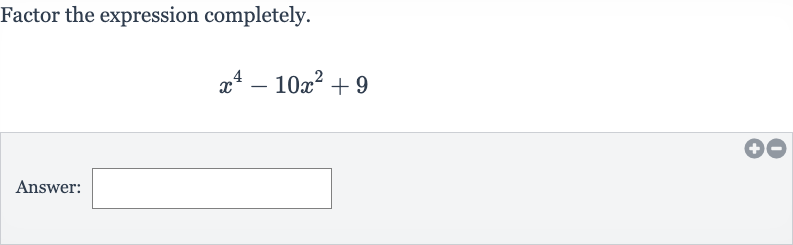
Factor the expression completely. x^(4)-10x^(2)+9 Answer:

Question

Factor the expression completely.  x^(4)-10x^(2)+9 Answer:

Bytelearn · Accepted Answer

Recognize Structure: Recognize the structure of the expression. The expression x^4 - 10x^2 + 9 is a quadratic in form, with x^2 taking the place of x in a standard quadratic equation. We can treat x^2 as a single variable and factor the expression as if it were a quadratic.Factor Quadratic Expression: Factor the quadratic expression. We are looking for two numbers that multiply to 9 and add up to -10. These numbers are -9 and -1 because (-9) * (-1) = 9 and (-9) + (-1) = -10. So, we can write the expression as (x^2 - 9)(x^2 - 1).Recognize Differences of Squares: Recognize that both factors are differences of squares. The expressions x^2 - 9 and x^2 - 1 are both differences of squares, which can be factored further.Factor Each Difference: Factor each difference of squares. The factor x^2 - 9 can be factored as (x + 3)(x - 3) because x^2 - 9 = (x + 3)(x - 3). The factor x^2 - 1 can be factored as (x + 1)(x - 1) because x^2 - 1 = (x + 1)(x - 1).Write Completely Factored Expression: Write the completely factored expression. Combining the factors from the previous steps, the completely factored form of the expression is (x + 3)(x - 3)(x + 1)(x - 1).

Factor the expression completely. $\newline$ $x^{4}-10 x^{2}+9$ $\newline$ Answer:

Full solution

More problems from Operations with rational exponents

Related topics

Factor the expression completely.\newlinex4−10x2+9 x^{4}-10 x^{2}+9 x4−10x2+9\newlineAnswer:

Factor the expression completely. $\newline$ $x^{4}-10 x^{2}+9$ $\newline$ Answer: