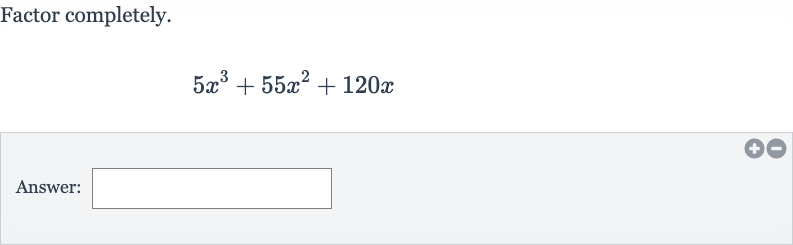Factor completely. 5x^(3)+55x^(2)+120 x Answer:

Question

Factor completely.  5x^(3)+55x^(2)+120 x Answer:

Bytelearn · Accepted Answer

Identify GCF: Identify the greatest common factor (GCF) of the terms in the polynomial 5x^3 + 55x^2 + 120x. The GCF of 5x^3, 55x^2, and 120x is 5x, since each term is divisible by 5x. Factor out the GCF from each term.Factor out GCF: Write the polynomial as a product of the GCF and the remaining terms. 5x^3 + 55x^2 + 120x = 5x(x^2 + 11x + 24) Check that the terms inside the parentheses are correct by distributing 5x back to each term. 5x(x^2) + 5x(11x) + 5x(24) = 5x^3 + 55x^2 + 120x, which matches the original polynomial.Write as product: Factor the quadratic expression inside the parentheses. The quadratic x^2 + 11x + 24 can be factored into two binomials because it is a simple trinomial. Find two numbers that multiply to 24 and add to 11. These numbers are 8 and 3. Write the factored form of the quadratic: (x + 8)(x + 3).Factor quadratic: Combine the GCF with the factored quadratic to write the completely factored form of the original polynomial. 5x^3 + 55x^2 + 120x = 5x(x + 8)(x + 3) Check that the factored form is correct by expanding the binomials and multiplying by 5x to see if it gives the original polynomial. 5x(x + 8)(x + 3) = 5x(x^2 + 11x + 24) = 5x^3 + 55x^2 + 120x, which is correct.

Factor completely. $\newline$ $5 x^{3}+55 x^{2}+120 x$ $\newline$ Answer:

Full solution

More problems from Operations with rational exponents

Related topics

Factor completely.\newline5x3+55x2+120x 5 x^{3}+55 x^{2}+120 x 5x3+55x2+120x\newlineAnswer:

Factor completely. $\newline$ $5 x^{3}+55 x^{2}+120 x$ $\newline$ Answer: