AI tutor
Full solution
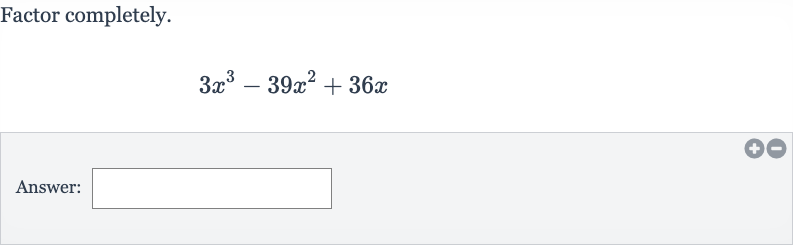
Q. Factor completely.Answer:
- Identify Common Factor: First, we look for a common factor in all three terms of the polynomial . We can see that each term has a factor of , so we factor out from each term.
- Factor Quadratic Expression: Now we need to factor the quadratic expression . We look for two numbers that multiply to (the constant term) and add up to (the coefficient of the term).The numbers that satisfy these conditions are and , since and .Therefore, we can factor the quadratic as .
- Check Factoring and Correct Mistake: We check our factoring by expanding the factors to see if we get the original polynomial. Expanding further, we get , which is not the original polynomial.We made a mistake in the previous step; the correct numbers should add up to , not .
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help