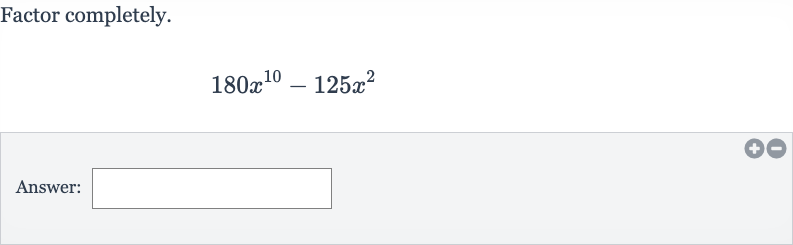
Factor completely. 180x^(10)-125x^(2) Answer:

Question

Factor completely.  180x^(10)-125x^(2) Answer:

Bytelearn · Accepted Answer

Identify GCF: Identify the greatest common factor (GCF) of the terms 180x^(10) and 125x^(2). The GCF of the numerical coefficients 180 and 125 is 5. The GCF of the variable terms x^(10) and x^(2) is x^(2), since x^(2) is the highest power of x that divides both terms. Therefore, the GCF of the entire expression is 5x^(2).Factor out GCF: Factor out the GCF from the expression. 180x^(10) - 125x^(2) = 5x^(2)(36x^(8) - 25)Find further factorization: Look for further factorization within the parentheses. The expression inside the parentheses, 36x^(8) - 25, is a difference of squares since 36x^(8) is a perfect square (6x^(4))^2 and 25 is a perfect square (5)^2. The difference of squares can be factored as (a^2 - b^2) = (a + b)(a - b).Apply difference of squares: Apply the difference of squares factorization to the expression inside the parentheses. 36x^(8) - 25 = (6x^(4))^2 - (5)^2 = (6x^(4) + 5)(6x^(4) - 5)Combine with GCF: Combine the GCF with the factored form of the expression inside the parentheses. 5x^(2)(36x^(8) - 25) = 5x^(2)(6x^(4) + 5)(6x^(4) - 5)

Factor completely. $\newline$ $180 x^{10}-125 x^{2}$ $\newline$ Answer:

Full solution

More problems from Operations with rational exponents

Related topics

Factor completely.\newline180x10−125x2 180 x^{10}-125 x^{2} 180x10−125x2\newlineAnswer:

Factor completely. $\newline$ $180 x^{10}-125 x^{2}$ $\newline$ Answer: