Full solution
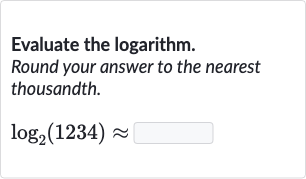
Q. Evaluate the logarithm.Round your answer to the nearest thousandth.
- Understand the problem: Understand the problem.We need to find the value of the logarithm of with base , which is written as . This means we are looking for the power to which must be raised to get .
- Use calculator or properties: Use a calculator or logarithm properties to evaluate . Since is not a power of , and the logarithm does not simplify easily, we will use a calculator to find the approximate value of . Using a calculator, we find that .
- Round to nearest thousandth: Round the result to the nearest thousandth.Rounding to the nearest thousandth gives us , as there are no additional digits to consider for further rounding.
More problems from Compare linear, exponential, and quadratic growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help