Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Circle O shown below has a radius of 25 inches. Find, to the nearest tenth, the radian measure of the angle, x, that forms an arc whose length is 18 inches. Answer: radians

Circle O O shown below has a radius of 2525 inches. Find, to the nearest tenth, the radian measure of the angle, x x , that forms an arc whose length is 1818 inches.\newlineAnswer: □\square radians

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find the radius or diameter of a circleright chevron icon

Full solution

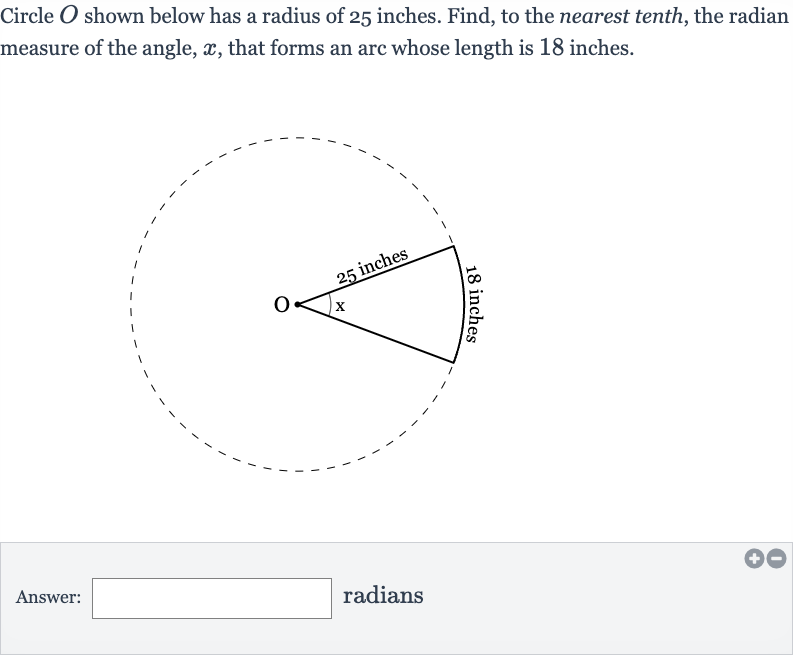
Q. Circle O O shown below has a radius of 2525 inches. Find, to the nearest tenth, the radian measure of the angle, x x , that forms an arc whose length is 1818 inches.\newlineAnswer: □\square radians
  1. Understand Relationship: Understand the relationship between arc length, radius, and central angle in radians. The formula that relates arc length ss, radius rr, and central angle in radians θ\theta is s=rθs = r\theta.
  2. Plug in Values: Plug in the given values into the formula.\newlineWe are given the arc length s=18s = 18 inches and the radius r=25r = 25 inches. We need to find the angle θ\theta in radians.\newlineSo, 18=25θ18 = 25\theta.
  3. Solve for θ\theta: Solve for θ\theta.\newlineTo find θ\theta, we divide both sides of the equation by 2525.\newlineθ=1825\theta = \frac{18}{25}.
  4. Calculate θ\theta: Calculate the value of θ\theta.θ=1825=0.72\theta = \frac{18}{25} = 0.72 radians.
  5. Round Answer: Round the answer to the nearest tenth. θ≈0.7\theta \approx 0.7 radians (to the nearest tenth).

More problems from Find the radius or diameter of a circle

Question
Write the equation in standard form for the circle x2+y2−9=0x^2+y^2-9=0.\newline_____
Get tutor helpright-arrow

Posted 9 months ago

Question
Write the equation in standard form for the circle with radius 22 centered at the origin.\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the center of the circle x2+y2−4=0x^2 + y^2 - 4 = 0?\newlineSimplify any fractions.\newline(_____,______)
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the center of the circle x2+y2=144x^2 + y^2 = 144??\newlineSimplify any fractions.\newline(__,__)\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the radius of the circle x2+y2=36x^2 + y^2 = 36?\newlineSimplify any fractions.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
Write the equation in standard form for the circle with radius 1111 centered at the origin. ______
Get tutor helpright-arrow

Posted 9 months ago

Question
Write the equation in standard form for the circle x2+y2+6x−1=0x^2+y^2+6x-1= 0.
Get tutor helpright-arrow

Posted 10 months ago

Question
Write the equation in standard form for the circle x2+y2−4x+7=0x^2+y^2-4x+7= 0.
Get tutor helpright-arrow

Posted 10 months ago

Question
Write the equation in standard form for the circle x2+y2−16=0x^2+y^2-16= 0.
Get tutor helpright-arrow

Posted 10 months ago

Question
Write the equation in standard form for the circle x2+y2+10y−25=0x^2+y^2+10y-25= 0.
Get tutor helpright-arrow

Posted 10 months ago

View all (24)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant