AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
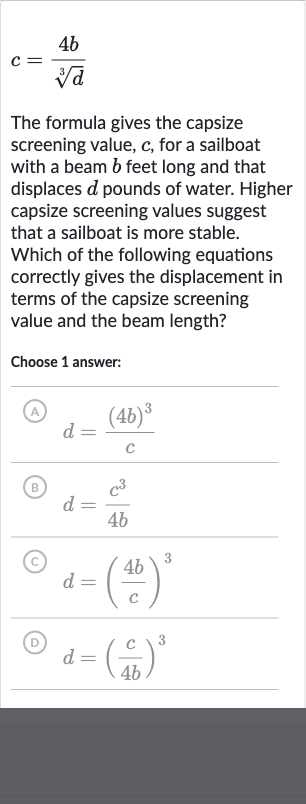
The formula gives the capsize screening value, , for a sailboat with a beam feet long and that displaces pounds of water. Higher capsize screening values suggest that a sailboat is more stable. Which of the following equations correctly gives the displacement in terms of the capsize screening value and the beam length?Choose answer:(A) (B) (C) (D)
Full solution
Q. The formula gives the capsize screening value, , for a sailboat with a beam feet long and that displaces pounds of water. Higher capsize screening values suggest that a sailboat is more stable. Which of the following equations correctly gives the displacement in terms of the capsize screening value and the beam length?Choose answer:(A) (B) (C) (D)
- Given formula isolation: The original formula is given by . We want to solve for in terms of and .
- Multiplication and isolation: First, we isolate the term with on one side by multiplying both sides of the equation by . This gives us .
- Division by : Next, we divide both sides of the equation by to get = .
- Eliminating cube root: To solve for , we need to get rid of the cube root. We do this by raising both sides of the equation to the power of , which gives us .
- Comparison with options: Now we compare the result with the given options. The correct equation that matches our result is (C) .
More problems from Compare linear and exponential growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
