Full solution
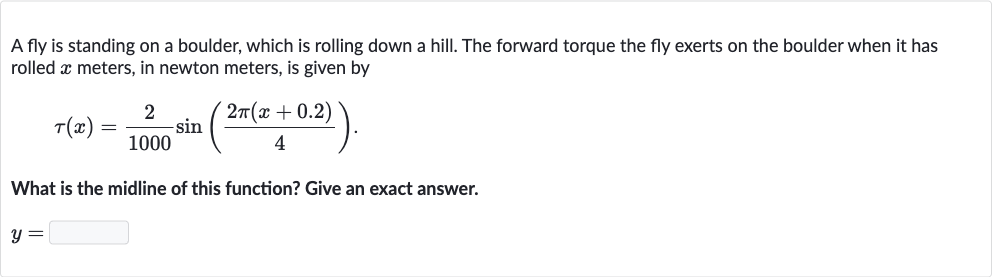
Q. A fly is standing on a boulder, which is rolling down a hill. The forward torque the fly exerts on the boulder when it has rolled meters, in newton meters, is given byWhat is the midline of this function? Give an exact answer.
- Calculate Midline: The midline of a sinusoidal function is the average of its maximum and minimum values, which is also the vertical shift in the function .
- Identify Vertical Shift: In the given function , there is no vertical shift, so .
- Final Midline: Therefore, the midline of the function is .
More problems from Write equations of cosine functions using properties
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help