A circle has a circumference of $4\pi \, \text{ft}$ . An arc, $x$ , in this circle has a central angle of $240^{\circ}$ . What is the length of $x$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{4\pi}{3}\,\text{ft}$ $\newline$ (B) $\frac{8\pi}{3}\,\text{ft}$ $\newline$ (C) $480\,\text{ft}$ $\newline$ (D) $960\,\text{ft}$

Full solution

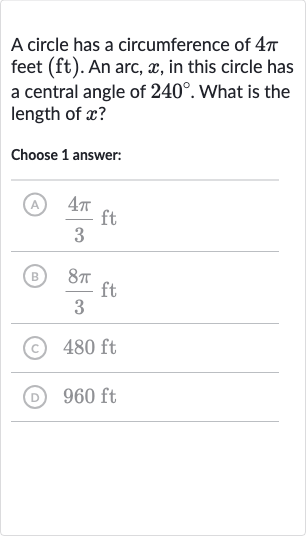
Q. A circle has a circumference of

4\pi \, \text{ft}

. An arc,

x

, in this circle has a central angle of

240^{\circ}

. What is the length of

x

\newline

Choose

1

answer:

\newline

(A)

\frac{4\pi}{3}\,\text{ft}

\newline

(B)

\frac{8\pi}{3}\,\text{ft}

\newline

(C)

480\,\text{ft}

\newline

(D)

960\,\text{ft}

Calculate Circumference Radius: The circumference of a circle is given by the formula $C = 2\pi r$ , where $r$ is the radius of the circle. We are given that the circumference is $4\pi$ feet, so we can solve for the radius $r$ . $4\pi = 2\pi r$ $r = \frac{4\pi}{2\pi}$ $r = 2$ feet
Convert Central Angle: The length of an arc $s$ in a circle is given by the formula $s = r\theta$ , where $\theta$ is the central angle in radians and $r$ is the radius. We need to convert the central angle from degrees to radians. The conversion factor is $\pi$ radians = $180$ degrees. $\newline$ $\theta = 240^\circ \times (\pi/180^\circ)$ $\newline$ $\theta = 4\pi/3$ radians
Calculate Arc Length: Now we can calculate the length of the arc $x$ using the radius $r = 2$ feet and the central angle $\theta = \frac{4\pi}{3}$ radians. $\newline$ $s = r\theta$ $\newline$ $s = 2 \text{ feet} \times \left(\frac{4\pi}{3} \text{ radians}\right)$ $\newline$ $s = \left(\frac{8\pi}{3}\right) \text{ feet}$