Full solution
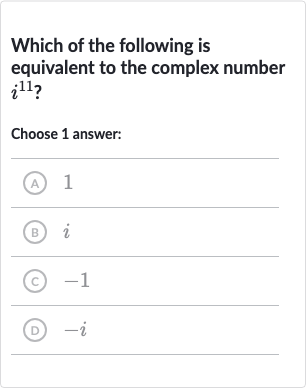
Q. Which of the following is equivalent to the complex number ?Choose answer:(A) (B) (C) (D)
- Introduction: To solve for , we need to remember that is the imaginary unit, which is defined by . We can use this property to simplify . Since , we can rewrite as .Now we simplify .Since raised to an odd power is , we have:
More problems from Domain and range of quadratic functions: equations
QuestionGet tutor help