Full solution
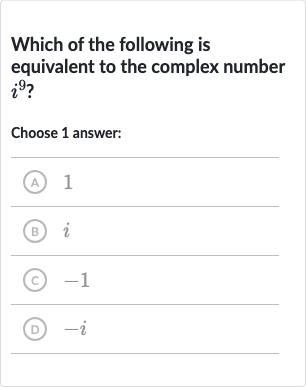
Q. Which of the following is equivalent to the complex number ?Choose answer:(A) (B) (C) (D)
- Complex number definition: To find the equivalent of the complex number , we need to remember that is the imaginary unit, which is defined by . We can simplify by breaking it down into powers of and the remaining factor of .
- Simplifying : Now we simplify . Since , we have:
- Calculating : We calculate . Any even power of is , so:
- Multiplying by i: Now we multiply the result by the remaining factor of i:
- Final result: Therefore, is equivalent to . The correct answer from the given choices is (B) .
More problems from Domain and range of quadratic functions: equations
QuestionGet tutor help