Full solution
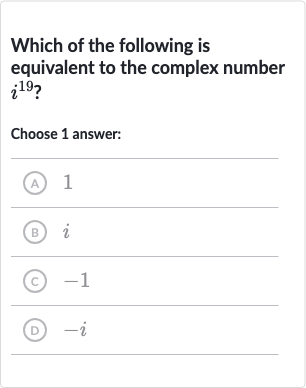
Q. Which of the following is equivalent to the complex number ?Choose answer:(A) (B) (C) (D)
- Definition of i: To solve for , we need to remember that is the imaginary unit, which is defined by . We can use the powers of to simplify by finding a pattern.
- Pattern of powers of i: The powers of i repeat in a cycle: , , , and . Then the cycle repeats because , , and so on.
- Finding : To find , we can divide by to find how many full cycles of there are and what the remainder is. The remainder will tell us the equivalent power of that we need to find. remainder . This means is equivalent to , which is the same as .
- Simplifying : Since is a full cycle repeated times, it is equivalent to . So we only need to consider ..
- Final result: Therefore, is equivalent to , which simplifies to , or just .
More problems from Domain and range of quadratic functions: equations
QuestionGet tutor help