The graph of $y=f(x)$ is a parabola in the $x y$ -plane that is symmetric with respect to the line $x=-2$ . The $y$ -coordinate of the vertex of the graph of $f$ is a maximum function value. Which of the following equations could represent function $f$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $f(x)=5(x-2)^{2}+3$ $\newline$ (B) $f(x)=5(x+2)^{2}+3$ $\newline$ (C) $f(x)=-5(x-2)^{2}+3$ $\newline$ (D) $f(x)=-5(x+2)^{2}+3$

View step-by-step help

Home

Math Problems

Algebra 1

Compare linear and exponential growth

Full solution

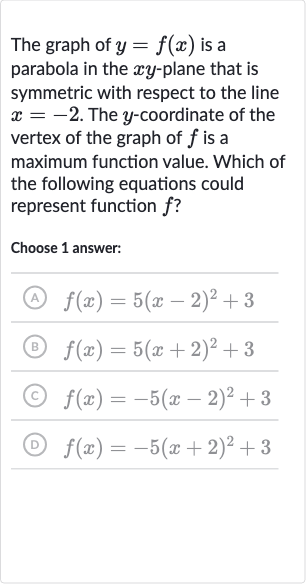
Q. The graph of

y=f(x)

is a parabola in the

x y

-plane that is symmetric with respect to the line

x=-2

. The

y

-coordinate of the vertex of the graph of

f

is a maximum function value. Which of the following equations could represent function

f

\newline

Choose

1

answer:

\newline

(A)

f(x)=5(x-2)^{2}+3

\newline

(B)

f(x)=5(x+2)^{2}+3

\newline

(C)

f(x)=-5(x-2)^{2}+3

\newline

(D)

f(x)=-5(x+2)^{2}+3

Identify Parabola Form: Identify the general form of a parabola with its vertex at the point $(h, k)$ . The general form of a parabola is given by $y = a(x - h)^2 + k$ , where $(h, k)$ is the vertex of the parabola. If the parabola opens upwards, $a$ is positive, and if it opens downwards, $a$ is negative. Since the y-coordinate of the vertex is a maximum, the parabola opens downwards, which means $a$ should be negative.
Determine Symmetry Line: Determine the value of $h$ from the symmetry line. $\newline$ The line of symmetry of the parabola is given by $x = h$ . Since the parabola is symmetric with respect to the line $x = -2$ , the value of $h$ is $-2$ .
Eliminate Incorrect Options: Eliminate the options that do not have the correct vertex form with $h = -2$ . $\newline$ Option (A) $f(x) = 5(x - 2)^2 + 3$ has $h = 2$ , which does not match the required line of symmetry $x = -2$ . $\newline$ Option (B) $f(x) = 5(x + 2)^2 + 3$ has $h = -2$ , which matches the required line of symmetry. $\newline$ Option (C) $f(x) = -5(x - 2)^2 + 3$ has $h = 2$ , which does not match the required line of symmetry $x = -2$ . $\newline$ Option (D) $f(x) = -5(x + 2)^2 + 3$ has $h = -2$ , which matches the required line of symmetry.
Identify Parabola Direction: Identify the correct option based on the direction of the parabola. $\newline$ Since the $y$ -coordinate of the vertex is a maximum, the parabola must open downwards, which means $a$ should be negative. This eliminates option (B) because it has a positive $a$ value.
Choose Correct Answer: Choose the correct answer from the remaining options. $\newline$ Option (D) $f(x) = -5(x + 2)^2 + 3$ is the only remaining option that satisfies both conditions: it has the correct line of symmetry ( $h = -2$ ) and the correct direction of the parabola ( $a$ is negative).