The expression $\newline$ $\left(y^{2}-t^{2}\right)(y+k)$ $\newline$ can be written as $\newline$ $y^{3}+36 y^{2}-9 y+s$ $\newline$ where $t, k$ , and $s$ are constants. What is the value of $s$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-324$ $\newline$ (B) $-54$ $\newline$ (C) $54$ $\newline$ (D) $324$

View step-by-step help

Home

Math Problems

Algebra 1

Compare linear and exponential growth

Full solution

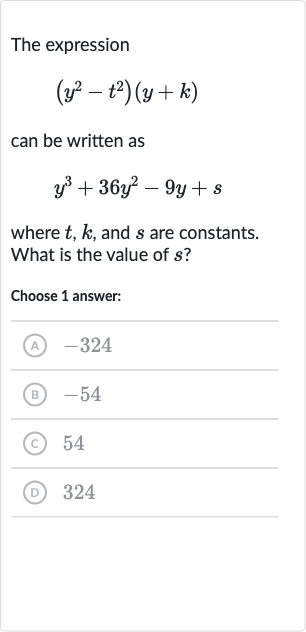
Q. The expression

\newline

\left(y^{2}-t^{2}\right)(y+k)

\newline

can be written as

\newline

y^{3}+36 y^{2}-9 y+s

\newline

where

t, k

, and

s

are constants. What is the value of

s

\newline

Choose

1

answer:

\newline

(A)

-324

\newline

(B)

-54

\newline

(C)

54

\newline

(D)

324

Expand and Compare: We need to expand the expression $(y^2 - t^2)(y + k)$ and compare it to the given expression $y^3 + 36y^2 - 9y + s$ to find the value of $s$ .
Factor Difference of Squares: First, recognize that $y^2 - t^2$ is a difference of squares and can be factored into $(y + t)(y - t)$ .
Distribute Across Binomial: Now, distribute $(y + t)(y - t)$ across $(y + k)$ to get the expanded form. Start with the first term of the first binomial $(y + t)$ : $(y + t)(y^2 - t^2) = y(y^2 - t^2) + t(y^2 - t^2).$
Expand $y(y^2 - t^2)$ : Expanding $y(y^2 - t^2)$ gives us $y^3 - yt^2$ .
Expand $t(y^2 - t^2)$ : Expanding $t(y^2 - t^2)$ gives us $ty^2 - t^3$ .
Add $k(y^2 - t^2)$ : Now, add $k(y^2 - t^2)$ to the expression: $y^3 - yt^2 + ty^2 - t^3 + k(y^2 - t^2)$ .
Combine Like Terms: Expanding $k(y^2 - t^2)$ gives us $ky^2 - kt^2$ .
Compare Coefficients: Combine like terms to get the full expanded expression: $y^3 + (ty^2 + ky^2) - yt^2 - t^3 - kt^2$ .
Solve for $t$ : Now, we compare the coefficients of the expanded expression to the given expression $y^3 + 36y^2 - 9y + s$ . We see that the coefficient of $y^2$ in the expanded expression is $t + k$ , which must be equal to $36$ in the given expression.
Substitute $t$ into Equation: We also see that the coefficient of $y$ in the expanded expression is $-yt$ , which must be equal to $-9$ in the given expression. This gives us the equation $-yt = -9$ .
Find Value of s: From the equation $-yt = -9$ , we can solve for $t$ by dividing both sides by $-y$ (assuming $y \neq 0$ ). This gives us $t = \frac{9}{y}$ .
Compare Constant Terms: Now, we substitute $t = \frac{9}{y}$ into the equation $t + k = 36$ to find the value of $k$ . This gives us $\frac{9}{y} + k = 36$ .
Compare Constant Terms: Now, we substitute $t = \frac{9}{y}$ into the equation $t + k = 36$ to find the value of $k$ . This gives us $\frac{9}{y} + k = 36$ .Since we cannot solve for $k$ without knowing the value of $y$ , we look at the constant terms in the expanded expression and the given expression. The constant term in the expanded expression is $-t^3 - kt^2$ , which must be equal to $s$ in the given expression.
Compare Constant Terms: Now, we substitute $t = \frac{9}{y}$ into the equation $t + k = 36$ to find the value of $k$ . This gives us $\frac{9}{y} + k = 36$ .Since we cannot solve for $k$ without knowing the value of $y$ , we look at the constant terms in the expanded expression and the given expression. The constant term in the expanded expression is $-t^3 - kt^2$ , which must be equal to $s$ in the given expression.We know that $t = \frac{9}{y}$ , so we substitute this into the constant term $-t^3 - kt^2$ to find $s$ . This gives us $t + k = 36$ $1$ .
Compare Constant Terms: Now, we substitute $t = \frac{9}{y}$ into the equation $t + k = 36$ to find the value of $k$ . This gives us $\frac{9}{y} + k = 36$ . Since we cannot solve for $k$ without knowing the value of $y$ , we look at the constant terms in the expanded expression and the given expression. The constant term in the expanded expression is $-t^3 - kt^2$ , which must be equal to $s$ in the given expression. We know that $t = \frac{9}{y}$ , so we substitute this into the constant term $-t^3 - kt^2$ to find $s$ . This gives us $t + k = 36$ $1$ . However, we made a mistake in the previous step. We do not need to substitute $t = \frac{9}{y}$ into the constant term because we are looking for the value of $s$ , which is the constant term in the given expression $t + k = 36$ $4$ . We should directly compare the constant terms from the expanded expression and the given expression.