AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
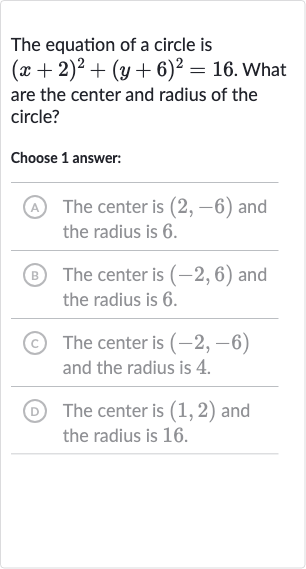
The equation of a circle is . What are the center and radius of the circle?Choose answer:(A) The center is and the radius is .(B) The center is and the radius is .(C) The center is and the radius is .(D) The center is and the radius is .
Full solution
Q. The equation of a circle is . What are the center and radius of the circle?Choose answer:(A) The center is and the radius is .(B) The center is and the radius is .(C) The center is and the radius is .(D) The center is and the radius is .
- Circle Equation Form: The general form of the equation of a circle is , where is the center of the circle and is the radius.
- Compare Given Equation: Compare the given equation and the radius .
- Find Center and Radius: The given equation can be rewritten as and . Therefore, the center of the circle is .
- Calculate Radius: To find the radius , we look at the right side of the equation, which is . Since the general form is , we take the square root of to find . The square root of is , so the radius is .
More problems from Compare linear and exponential growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
