Full solution
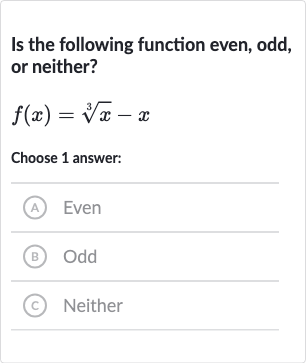
Q. Is the following function even, odd, or neither?Choose answer:(A) Even(B) Odd(C) Neither
- Determining Function Symmetry: To determine if the function is even, odd, or neither, we need to check the symmetry properties of the function. A function is even if for all in the domain, and it is odd if for all in the domain.
- Checking for Even Symmetry: First, let's check if the function is even. We calculate and see if it is equal to .Now we compare this to :Clearly, is not equal to , so the function is not even.
- Checking for Odd Symmetry: Next, let's check if the function is odd. We calculate and see if it is equal to .We already have from the previous step:Now we calculate :We see that is equal to , so the function is odd.