Full solution
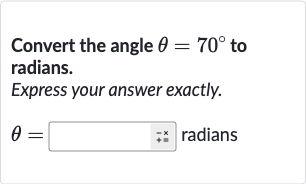
Q. Convert the angle to radians.Express your answer exactly.
- Understanding degrees and radians: Understand the relationship between degrees and radians.One complete revolution is , which is equivalent to radians. Therefore, to convert degrees to radians, we use the conversion factor .
- Setting up the conversion: Set up the conversion for degrees to radians using the relationship from Step .
- Substituting values: Substitute for in degrees into the conversion formula. in radians =
- Simplifying the expression: Simplify the expression by multiplying by and then dividing by . in radians =
- Reducing the fraction: Reduce the fraction to its simplest form.Both and are divisible by , so we can simplify the fraction by dividing both the numerator and the denominator by . in radians =