Full solution
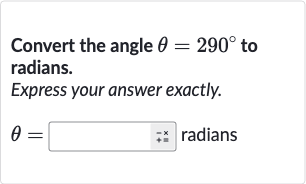
Q. Convert the angle to radians.Express your answer exactly.
- Understanding degrees and radians: Understand the relationship between degrees and radians.One complete revolution () is equal to radians. Therefore, to convert degrees to radians, we use the conversion factor .
- Setting up the conversion: Set up the conversion from degrees to radians for . in radians = in degrees
- Substituting the given value: Substitute the given value of in degrees into the conversion formula. in radians = degrees
- Performing the multiplication: Perform the multiplication to find in radians. in radians = in radians =
- Simplifying the fraction: Simplify the fraction if possible.The fraction cannot be simplified further, so the exact value of theta in radians is .