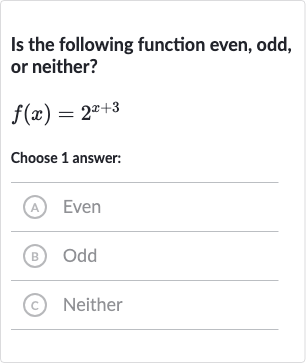
Is the following function even, odd, or neither? f(x)=2^(x+3) Choose 1 answer: A) Even (B) Odd (c) Neither

Question

Is the following function even, odd, or neither?  f(x)=2^(x+3) Choose 1 answer: A) Even (B) Odd (c) Neither

Bytelearn · Accepted Answer

Symmetry properties of the function: To determine if the function f(x) = 2^(x+3) is even, odd, or neither, we need to check the symmetry properties of the function. An even function satisfies f(x) = f(-x) for all x in its domain, and an odd function satisfies f(-x) = -f(x) for all x in its domain.Checking if f(x) is even: Let's first check if f(x) is even. We need to compare f(x) with f(-x). We have f(x) = 2^(x+3). Now let's find f(-x) which is f(-x) = 2^(-x+3).Comparing f(x) with f(-x): Now we compare f(x) with f(-x). If f(x) = f(-x) for all x, then the function is even. We have f(x) = 2^(x+3) and f(-x) = 2^(-x+3). These two expressions are not equal for all x because the exponents are not the same due to the sign change in x. Therefore, f(x) is not an even function.Conclusion: f(x) is not an even function: Next, let's check if f(x) is odd. For f(x) to be odd, we need f(-x) to be equal to -f(x) for all x. We already have f(-x) = 2^(-x+3). Now let's find -f(x) which is -f(x) = -2^(x+3).Checking if f(x) is odd: We compare f(-x) with -f(x). If f(-x) = -f(x) for all x, then the function is odd. We have f(-x) = 2^(-x+3) and -f(x) = -2^(x+3). These two expressions are not equal for all x because the negative sign outside the exponent does not change the exponent itself. Therefore, f(x) is not an odd function.Comparing f(-x) with -f(x): Since f(x) is neither even nor odd, the correct choice is (C) Neither.

Is the following function even, odd, or neither? $\newline$ $f(x)=2^{x+3}$ $\newline$ Choose $1$ answer: $\newline$ (A) Even $\newline$ (B) Odd $\newline$ (C) Neither

Full solution

More problems from Symmetry and periodicity of trigonometric functions

Related topics

Is the following function even, odd, or neither?\newlinef(x)=2x+3 f(x)=2^{x+3} f(x)=2x+3\newlineChoose 111 answer:\newline(A) Even\newline(B) Odd\newline(C) Neither

Is the following function even, odd, or neither? $\newline$ $f(x)=2^{x+3}$ $\newline$ Choose $1$ answer: $\newline$ (A) Even $\newline$ (B) Odd $\newline$ (C) Neither