Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If
2^(m)=x and
7^(n)=y, then which of the following is equivalent to
784^(mn) ?
Choose 1 answer:
(A)
x^(2m)*y^(4n)
(B)
x^(2n)*y^(4m)
(C)
x^(4m)*y^(2n)
(D)
x^(4n)*y^(2m)

If $2^{m}=x$ and $7^{n}=y$ , then which of the following is equivalent to $784^{m n}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $x^{2 m} \cdot y^{4 n}$ $\newline$ (B) $x^{2 n} \cdot y^{4 m}$ $\newline$ (C) $x^{4 m} \cdot y^{2 n}$ $\newline$ (D) $x^{4 n} \cdot y^{2 m}$

View step-by-step help

View step-by-step help

Compare linear and exponential growth

Full solution

Q. If

2^{m}=x

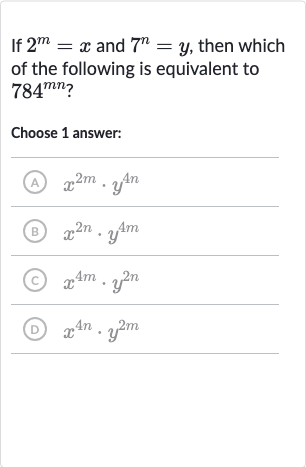
and

7^{n}=y

, then which of the following is equivalent to

784^{m n}

?

\newline

Choose

1

answer:

\newline

(A)

x^{2 m} \cdot y^{4 n}

\newline

(B)

x^{2 n} \cdot y^{4 m}

\newline

(C)

x^{4 m} \cdot y^{2 n}

\newline

(D)

x^{4 n} \cdot y^{2 m}

Expressing $784$ as Prime Factors: First, let's express $784$ as a product of its prime factors. $\newline$ $784 = 2^4 \times 7^2$ $\newline$ This is because $784$ is divisible by $2$ four times ( $2 \times 2 \times 2 \times 2 = 16$ ) and by $7$ twice ( $7 \times 7 = 49$ ), and $16 \times 49 = 784$ .
Raising Prime Factorization to Power: Now, let's raise this prime factorization to the power of $mn$ : $\newline$ $(2^4 \times 7^2)^{mn} = (2^{4mn}) \times (7^{2mn})$ $\newline$ We distribute the exponent $mn$ to both $2^4$ and $7^2$ .
Substituting Variables: Next, we substitute $x$ for $2^m$ and $y$ for $7^n$ according to the given information: $\newline$ $2^{m} = x$ and $7^{n} = y$ $\newline$ So, $2^{4mn}$ becomes $x^{4n}$ and $7^{2mn}$ becomes $y^{2m}$ .
Writing the Expression with Substituted Variables: Now, we write the expression with the substituted variables: $\newline$ $(2^{4mn}) \times (7^{2mn}) = x^{4n} \times y^{2m}$ $\newline$ This matches one of the answer choices.
Comparing with Answer Choices: We compare our expression with the answer choices: $\newline$ (A) $x^{2m} \cdot y^{4n}$ $\newline$ (B) $x^{2n} \cdot y^{4m}$ $\newline$ (C) $x^{4m} \cdot y^{2n}$ $\newline$ (D) $x^{4n} \cdot y^{2m}$ $\newline$ Our expression is $x^{4n} \cdot y^{2m}$ , which matches answer choice (D).

More problems from Compare linear and exponential growth

Question

Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits

x

days to pick up the motorcycle.

\newline

Write an equation for the function. If it is linear, write it in the form

g(x) = mx + b

. If it is exponential, write it in the form

g(x) = a(b)^x

\newline

g(x) = \underline{\hspace{3em}}

Posted 5 months ago

Question

f(t)=-2t-7

change over the interval from

t=-7

t=-6

\newline

\newline

\left[\text{f(t) decreases by } 2\right]

\newline

\left[\text{f(t) increases by } 2\right]

\newline

\left[\text{f(t) increases by } 200\%\right]

\newline

\left[\text{f(t) decreases by a factor of } 2\right]

Posted 5 months ago

Question

g(t)=9^t

change over the interval from

t=1

t=3

\newline

\newline

\left[\text{g(t) decreases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by } 18\%\right]

\newline

\left[\text{g(t) decreases by } 9\%\right]

Posted 5 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A)f(x) = 8x + 3.3

\newline

(B)g(x) = 3.3^x - 5

Posted 6 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A) \ f(x) = 2x + 9

\newline

(B)\ g(x) = 2^x

Posted 6 months ago

Question

f(x)

g(x)

are differentiable.

\newline

h(x)

h(x)=\frac{g(x)}{f(x)}

\newline

f(8)=1

f'(8)=-6

g(8)=8

g'(8)=-10

h'(8)

\newline

Simplify any fractions.

\newline

h'(8)=

Posted 6 months ago

Question

p(x)

q(x)

are differentiable.

\newline

r(x)

r(x)= \frac{p(x)}{q(x)}

\newline

p(3)= 2

p'(3)= 4

q(3)= 6

q'(3)= 9

r'(3)

\newline

Simplify any fractions.

\newline

r'(3)=

Posted 7 months ago

Question

u(x)

v(x)

are differentiable.

\newline

w(x)

w(x)= \frac{u(x)}{v(x)}

\newline

u(5)= 3

u'(5)= -2

v(5)= 7

v'(5)= 1

w'(5)

\newline

Simplify any fractions.

\newline

w'(5)=

Posted 7 months ago

Question

a(x)

b(x)

are differentiable.

\newline

c(x)

c(x)= \frac{a(x)}{b(x)}

\newline

a(2)= 4

a'(2)= 5

b(2)= 1

b'(2)= -3

c'(2)

\newline

Simplify any fractions.

\newline

c'(2)=

Posted 7 months ago

Question

m(x)

n(x)

are differentiable.

\newline

o(x)

o(x)= \frac{m(x)}{n(x)}

\newline

m(7)= 2

m'(7)= -1

n(7)= 4

n'(7)= 8

o'(7)

\newline

Simplify any fractions.

\newline

o'(7)=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant