Full solution
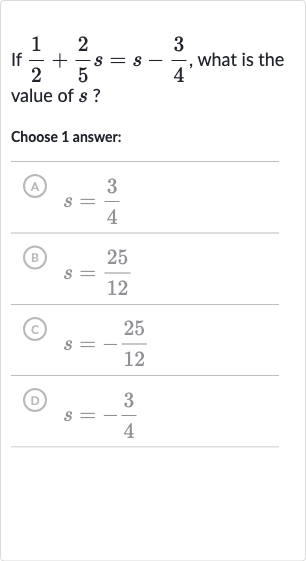
Q. If , what is the value of ?Choose answer:(A) (B) (C) (D)
- Write and Identify Equation: Write down the given equation and identify the type of problem.We have the equation . This is a linear equation in one variable, .
- Combine Like Terms: Combine like terms by moving all terms involving to one side of the equation and constants to the other side.Subtract from both sides to get all the terms on one side:.
- Find Common Denominator: Find a common denominator for the constants and combine them.The common denominator for and is , so we convert to :.
- Combine Constants: Combine the constants on the right side of the equation.This simplifies to:
- Combine Like Terms with : Combine like terms involving on the right side of the equation.To combine , we need a common denominator for the coefficients of , which is :This simplifies to:
- Solve for s: Solve for s by dividing both sides of the equation by the coefficient of s.Divide both sides by to isolate s:.
- Calculate Value of : Calculate the value of .To divide by a fraction, we multiply by its reciprocal:.This simplifies to:.
More problems from Compare linear and exponential growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help