Full solution
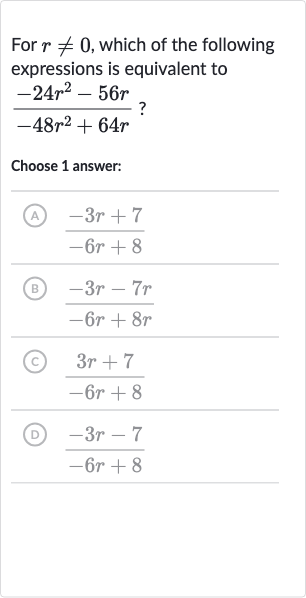
Q. For , which of the following expressions is equivalent to ?Choose answer:(A) (B) (C) (D)
- Identify common factor: Identify the common factor in both the numerator and the denominator.The common factor in the numerator is .The common factor in the denominator is .
- Factor out common factors: Factor out the common factors from the numerator and the denominator.Numerator: Denominator:
- Simplify expression: Simplify the expression by canceling out the common terms.The common term simplifies to .So, the expression becomes .
- Multiply by : Multiply the numerator and the denominator by to get rid of the fraction.The expression becomes .
- Distribute in denominator: Distribute the in the denominator.The expression becomes .
- Compare with answer choices: Compare the simplified expression with the answer choices.The simplified expression matches with choice (C).
More problems from Compare linear and exponential growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help