Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

An exponential function is graphed in the
xy-plane. If the graph of the function is always increasing and its
y-intercept is
(0,6), which of the following could be the equation of the function?
Choose 1 answer:
(A)
y=6(0.5)^(x)
(B)
y=12(0.5)^(x)
(C)
y=6(2)^(x)+1
(D)
y=4(2)^(x)+2

An exponential function is graphed in the $x y$ -plane. If the graph of the function is always increasing and its $y$ -intercept is $(0,6)$ , which of the following could be the equation of the function? $\newline$ Choose $1$ answer: $\newline$ (A) $y=6(0.5)^{x}$ $\newline$ (B) $y=12(0.5)^{x}$ $\newline$ (C) $y=6(2)^{x}+1$ $\newline$ (D) $y=4(2)^{x}+2$

View step-by-step help

View step-by-step help

Compare linear and exponential growth

Full solution

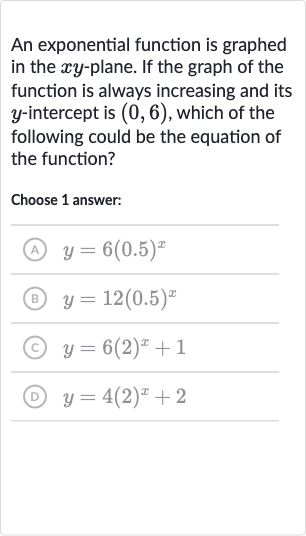
Q. An exponential function is graphed in the

x y

-plane. If the graph of the function is always increasing and its

y

-intercept is

(0,6)

, which of the following could be the equation of the function?

\newline

Choose

1

answer:

\newline

(A)

y=6(0.5)^{x}

\newline

(B)

y=12(0.5)^{x}

\newline

(C)

y=6(2)^{x}+1

\newline

(D)

y=4(2)^{x}+2

Exponential Function Behavior: An exponential function of the form $y = ab^x$ is always increasing if the base $b$ is greater than $1$ . This is because as $x$ increases, the value of $b^x$ increases when b > 1.
Finding Y-Intercept: The $y$ -intercept of a function is the value of $y$ when $x = 0$ . For an exponential function $y = ab^x$ , the $y$ -intercept is found by setting $x$ to $0$ , which gives $y = ab^0 = a$ . Therefore, the $y$ -intercept is $(0, a)$ .
Determining Correct Function: Given that the y-intercept is $(0,6)$ , we can determine that $a$ must be $6$ for the correct function. We can now check the options to see which one has a y-intercept of $6$ and a base greater than $1$ .
Option (A) Analysis: Option (A) $y=6(0.5)^x$ has a base of $0.5$ , which is less than $1$ . This means the function is decreasing, not increasing. Therefore, option (A) is not the correct function.
Option (B) Analysis: Option (B) $y=12(0.5)^x$ has a base of $0.5$ , which is less than $1$ . This means the function is decreasing, not increasing. Additionally, the $y$ -intercept is $12$ , not $6$ . Therefore, option (B) is not the correct function.
Option (C) Analysis: Option (C) $y=6(2)^x+1$ has a base of $2$ , which is greater than $1$ , indicating an increasing function. However, when $x = 0$ , $y = 6(2)^0 + 1 = 6(1) + 1 = 7$ , not $6$ . Therefore, option (C) does not have the correct $y$ -intercept.
Option (D) Analysis: Option (D) $y=4(2)^x+2$ has a base of $2$ , which is greater than $1$ , indicating an increasing function. However, when $x = 0$ , $y = 4(2)^0 + 2 = 4(1) + 2 = 6$ . This function has the correct y-intercept of $6$ . Therefore, option (D) is the correct function.

More problems from Compare linear and exponential growth

Question

Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits

x

days to pick up the motorcycle.

\newline

Write an equation for the function. If it is linear, write it in the form

g(x) = mx + b

. If it is exponential, write it in the form

g(x) = a(b)^x

\newline

g(x) = \underline{\hspace{3em}}

Posted 5 months ago

Question

f(t)=-2t-7

change over the interval from

t=-7

t=-6

\newline

\newline

\left[\text{f(t) decreases by } 2\right]

\newline

\left[\text{f(t) increases by } 2\right]

\newline

\left[\text{f(t) increases by } 200\%\right]

\newline

\left[\text{f(t) decreases by a factor of } 2\right]

Posted 5 months ago

Question

g(t)=9^t

change over the interval from

t=1

t=3

\newline

\newline

\left[\text{g(t) decreases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by } 18\%\right]

\newline

\left[\text{g(t) decreases by } 9\%\right]

Posted 5 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A)f(x) = 8x + 3.3

\newline

(B)g(x) = 3.3^x - 5

Posted 6 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A) \ f(x) = 2x + 9

\newline

(B)\ g(x) = 2^x

Posted 6 months ago

Question

f(x)

g(x)

are differentiable.

\newline

h(x)

h(x)=\frac{g(x)}{f(x)}

\newline

f(8)=1

f'(8)=-6

g(8)=8

g'(8)=-10

h'(8)

\newline

Simplify any fractions.

\newline

h'(8)=

Posted 6 months ago

Question

p(x)

q(x)

are differentiable.

\newline

r(x)

r(x)= \frac{p(x)}{q(x)}

\newline

p(3)= 2

p'(3)= 4

q(3)= 6

q'(3)= 9

r'(3)

\newline

Simplify any fractions.

\newline

r'(3)=

Posted 7 months ago

Question

u(x)

v(x)

are differentiable.

\newline

w(x)

w(x)= \frac{u(x)}{v(x)}

\newline

u(5)= 3

u'(5)= -2

v(5)= 7

v'(5)= 1

w'(5)

\newline

Simplify any fractions.

\newline

w'(5)=

Posted 7 months ago

Question

a(x)

b(x)

are differentiable.

\newline

c(x)

c(x)= \frac{a(x)}{b(x)}

\newline

a(2)= 4

a'(2)= 5

b(2)= 1

b'(2)= -3

c'(2)

\newline

Simplify any fractions.

\newline

c'(2)=

Posted 7 months ago

Question

m(x)

n(x)

are differentiable.

\newline

o(x)

o(x)= \frac{m(x)}{n(x)}

\newline

m(7)= 2

m'(7)= -1

n(7)= 4

n'(7)= 8

o'(7)

\newline

Simplify any fractions.

\newline

o'(7)=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant