Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A circle in the xy-plane has the equation x^(2)+y^(2)-14 y-51=0. What is the center of the circle? Choose 1 answer: (A) (51,14) (B) (7,10) (c) (0,0) (D) (0,7)

A circle in the xy x y -plane has the equation x2+y2−14y−51=0 x^{2}+y^{2}-14 y-51=0 . What is the center of the circle?\newlineChoose 11 answer:\newline(A) (51,14) (51,14) \newline(B) (7,10) (7,10) \newline(C) (0,0) (0,0) \newline(D) (0,7) (0,7)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find properties of circles from equations in general formright chevron icon

Full solution

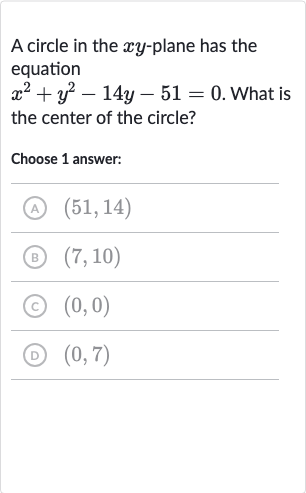
Q. A circle in the xy x y -plane has the equation x2+y2−14y−51=0 x^{2}+y^{2}-14 y-51=0 . What is the center of the circle?\newlineChoose 11 answer:\newline(A) (51,14) (51,14) \newline(B) (7,10) (7,10) \newline(C) (0,0) (0,0) \newline(D) (0,7) (0,7)
  1. Complete the square: First, we need to complete the square for the yy terms.x2+y2−14y=51x^2 + y^2 - 14y = 51To complete the square, take half of the coefficient of yy, square it, and add it to both sides.Half of −14 is −7, and (−7)2=49.\text{Half of } -14 \text{ is } -7, \text{ and } (-7)^2 = 49.So, we add 4949 to both sides.x2+y2−14y+49=51+49x^2 + y^2 - 14y + 49 = 51 + 49x2+(y−7)2=100x^2 + (y - 7)^2 = 100
  2. Circle equation form: Now, we have the equation of the circle in the form (x−h)2+(y−k)2=r2(x - h)^2 + (y - k)^2 = r^2, where (h,k)(h, k) is the center and rr is the radius.\newlineFrom the equation x2+(y−7)2=100x^2 + (y - 7)^2 = 100, we can see that h=0h = 0 and k=7k = 7.
  3. Center of the circle: So, the center of the circle is (h,k)=(0,7)(h, k) = (0, 7).

More problems from Find properties of circles from equations in general form

Question
Write the equation in standard form for the circle x2+y2−9=0x^2+y^2-9=0.\newline_____
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the equation in standard form for the circle with radius 22 centered at the origin.\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the center of the circle x2+y2−4=0x^2 + y^2 - 4 = 0?\newlineSimplify any fractions.\newline(_____,______)
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the center of the circle x2+y2=144x^2 + y^2 = 144??\newlineSimplify any fractions.\newline(__,__)\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the radius of the circle x2+y2=36x^2 + y^2 = 36?\newlineSimplify any fractions.\newline____
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the equation in standard form for the circle with radius 1111 centered at the origin. ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the equation in standard form for the circle x2+y2+6x−1=0x^2+y^2+6x-1= 0.
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the equation in standard form for the circle x2+y2−4x+7=0x^2+y^2-4x+7= 0.
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the equation in standard form for the circle x2+y2−16=0x^2+y^2-16= 0.
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the equation in standard form for the circle x2+y2+10y−25=0x^2+y^2+10y-25= 0.
Get tutor helpright-arrow

Posted 3 months ago

View all (13)