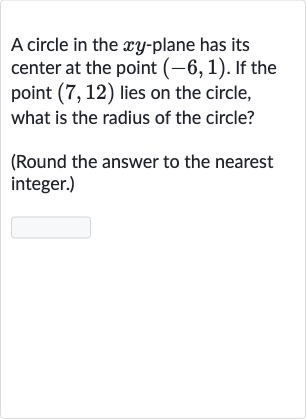
A circle in the xy-plane has its center at the point (-6,1). If the point (7,12) lies on the circle, what is the radius of the circle? (Round the answer to the nearest integer.)

Question

A circle in the  xy-plane has its center at the point  (-6,1). If the point  (7,12) lies on the circle, what is the radius of the circle? (Round the answer to the nearest integer.)

Bytelearn · Accepted Answer

Identify Center and Point: Identify the coordinates of the center of the circle and a point on the circle. The center of the circle is at (-6,1), and the point on the circle is (7,12).Calculate Radius: Use the distance formula to calculate the radius of the circle. The distance formula is $ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $, where $ (x_1, y_1) $ and $ (x_2, y_2) $ are the coordinates of two points.Plug Coordinates into Formula: Plug the coordinates of the center and the point on the circle into the distance formula. Using the center (-6,1) and the point (7,12), we get: $ r = \sqrt{(7 - (-6))^2 + (12 - 1)^2} $ $ r = \sqrt{(7 + 6)^2 + (12 - 1)^2} $ $ r = \sqrt{13^2 + 11^2} $ $ r = \sqrt{169 + 121} $ $ r = \sqrt{290} $Round to Nearest Integer: Round the result to the nearest integer. Since $ \sqrt{290} $ is approximately 17.03, we round it to the nearest integer, which is 17.

A circle in the $x y$ -plane has its center at the point $(-6,1)$ . If the point $(7,12)$ lies on the circle, what is the radius of the circle? $\newline$ (Round the answer to the nearest integer.)

Full solution

More problems from Find the radius or diameter of a circle

Related topics

A circle in the xy x y xy-plane has its center at the point (−6,1) (-6,1) (−6,1). If the point (7,12) (7,12) (7,12) lies on the circle, what is the radius of the circle?\newline(Round the answer to the nearest integer.)

A circle in the $x y$ -plane has its center at the point $(-6,1)$ . If the point $(7,12)$ lies on the circle, what is the radius of the circle? $\newline$ (Round the answer to the nearest integer.)