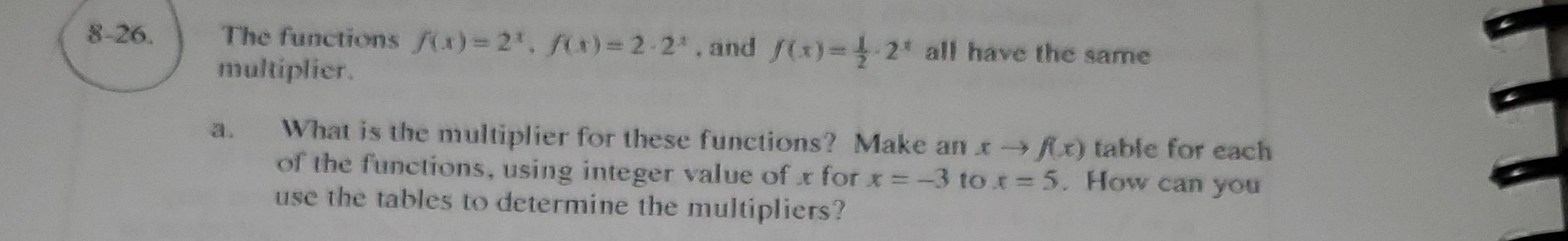Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

8-26. The functions f(x)=2^(x),f(x)=2*2^(x), and f(x)=(1)/(2)*2^(x) all have the same nuultiplier. a. What is the multiplier for these functions? Make an x rarr f(x) table for each of the functions, using integer value of x for x=-3 to x=5. How can you use the tables to determine the multipliers?

The functions f(x)=2x,f(x)=2⋅2x f(x)=2^{x}, f(x)=2 \cdot 2^{x} , and f(x)=12⋅2x f(x)=\frac{1}{2} \cdot 2^{x} all have the same nuultiplier.\newlinea. What is the multiplier for these functions? Make an x→f(x) x \rightarrow f(x) table for each of the functions, using integer value of x x for x=−3 x=-3 to x=5 x=5 . How can you use the tables to determine the multipliers?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Compare linear and exponential growthright chevron icon

Full solution

Q. The functions f(x)=2x,f(x)=2⋅2x f(x)=2^{x}, f(x)=2 \cdot 2^{x} , and f(x)=12⋅2x f(x)=\frac{1}{2} \cdot 2^{x} all have the same nuultiplier.\newlinea. What is the multiplier for these functions? Make an x→f(x) x \rightarrow f(x) table for each of the functions, using integer value of x x for x=−3 x=-3 to x=5 x=5 . How can you use the tables to determine the multipliers?
  1. Define Functions and Multiplier: Define the functions and identify the multiplier. \newlinef(x)=2xf(x) = 2^x, f(x)=2⋅2xf(x) = 2 \cdot 2^x, and f(x)=(12)⋅2xf(x) = (\frac{1}{2}) \cdot 2^x all involve the base 22 raised to the power xx. The multiplier in each function is the coefficient of 2x2^x.\newlineFor f(x)=2xf(x) = 2^x, the multiplier is 11.\newlineFor f(x)=2⋅2xf(x) = 2 \cdot 2^x, the multiplier is 22.\newlineFor f(x)=(12)⋅2xf(x) = (\frac{1}{2}) \cdot 2^x, the multiplier is f(x)=2⋅2xf(x) = 2 \cdot 2^x11.
  2. Create x⟶f(x)x \longrightarrow f(x) Table: Create an x⟶f(x)x \longrightarrow f(x) table for each function from x=−3x = -3 to x=5x = 5. For f(x)=2xf(x) = 2^x: x=−3⟶f(x)=2−3=18x = -3 \longrightarrow f(x) = 2^{-3} = \frac{1}{8} x=−2⟶f(x)=2−2=14x = -2 \longrightarrow f(x) = 2^{-2} = \frac{1}{4} x=−1⟶f(x)=2−1=12x = -1 \longrightarrow f(x) = 2^{-1} = \frac{1}{2} x=0⟶f(x)=20=1x = 0 \longrightarrow f(x) = 2^0 = 1 x=1⟶f(x)=21=2x = 1 \longrightarrow f(x) = 2^1 = 2 x⟶f(x)x \longrightarrow f(x)00 x⟶f(x)x \longrightarrow f(x)11 x⟶f(x)x \longrightarrow f(x)22 x⟶f(x)x \longrightarrow f(x)33
  3. Continue Table for 2⋅2x2\cdot2^x: Continue the table for f(x)=2⋅2xf(x) = 2\cdot2^x.\newlinex=−3⟶f(x)=2⋅2−3=14x = -3 \longrightarrow f(x) = 2\cdot2^{-3} = \frac{1}{4}\newlinex=−2⟶f(x)=2⋅2−2=12x = -2 \longrightarrow f(x) = 2\cdot2^{-2} = \frac{1}{2}\newlinex=−1⟶f(x)=2⋅2−1=1x = -1 \longrightarrow f(x) = 2\cdot2^{-1} = 1\newlinex=0⟶f(x)=2⋅20=2x = 0 \longrightarrow f(x) = 2\cdot2^0 = 2\newlinex=1⟶f(x)=2⋅21=4x = 1 \longrightarrow f(x) = 2\cdot2^1 = 4\newlinex=2⟶f(x)=2⋅22=8x = 2 \longrightarrow f(x) = 2\cdot2^2 = 8\newlinex=3⟶f(x)=2⋅23=16x = 3 \longrightarrow f(x) = 2\cdot2^3 = 16\newlinex=4⟶f(x)=2⋅24=32x = 4 \longrightarrow f(x) = 2\cdot2^4 = 32\newline$x = \(5\) \longrightarrow f(x) = \(2\)\cdot\(2\)^\(5\) = \(64\)
  4. Continue Table for \((1/2)\cdot2^x\): Continue the table for \(f(x) = (1/2)\cdot2^x\).
    \(x = -3 \rightarrow f(x) = (1/2)\cdot2^{-3} = 1/16\)
    \(x = -2 \rightarrow f(x) = (1/2)\cdot2^{-2} = 1/8\)
    \(x = -1 \rightarrow f(x) = (1/2)\cdot2^{-1} = 1/4\)
    \(x = 0 \rightarrow f(x) = (1/2)\cdot2^0 = 1/2\)
    \(x = 1 \rightarrow f(x) = (1/2)\cdot2^1 = 1\)
    \(x = 2 \rightarrow f(x) = (1/2)\cdot2^2 = 2\)
    \(x = 3 \rightarrow f(x) = (1/2)\cdot2^3 = 4\)
    \(x = 4 \rightarrow f(x) = (1/2)\cdot2^4 = 8\)
    \(f(x) = (1/2)\cdot2^x\)\(0\)
  5. Analyze Tables for Multipliers: Analyze the tables to determine the multipliers. By comparing the values of \(f(x)\) for each function at the same \(x\), we see that each function's output is a multiple of \(2^x\). The multiplier directly affects the output values, confirming the multipliers identified in Step \(1\).

More problems from Compare linear and exponential growth

Question
Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits xx days to pick up the motorcycle.\newlineWrite an equation for the function. If it is linear, write it in the form g(x)=mx+bg(x) = mx + b. If it is exponential, write it in the form g(x)=a(b)xg(x) = a(b)^x.\newlineg(x)=‾g(x) = \underline{\hspace{3em}}
Get tutor helpright-arrow

Posted 7 months ago

Question
How does f(t)=−2t−7f(t)=-2t-7 change over the interval from t=−7t=-7 to t=−6t=-6?\newlineChoices:\newline[f(t) decreases by 2]\left[\text{f(t) decreases by } 2\right]\newline[f(t) increases by 2]\left[\text{f(t) increases by } 2\right]\newline[f(t) increases by 200%]\left[\text{f(t) increases by } 200\%\right]\newline[f(t) decreases by a factor of 2]\left[\text{f(t) decreases by a factor of } 2\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
How does g(t)=9tg(t)=9^t change over the interval from t=1t=1 to t=3t=3?\newlineChoices: \newline[g(t) decreases by a factor of 81]\left[\text{g(t) decreases by a factor of } 81\right]\newline[g(t) increases by a factor of 81]\left[\text{g(t) increases by a factor of } 81\right]\newline[g(t) increases by 18%]\left[\text{g(t) increases by } 18\%\right]\newline[g(t) decreases by 9%]\left[\text{g(t) decreases by } 9\%\right]
Get tutor helpright-arrow

Posted 7 months ago

Question
Both of these functions grow as xx gets larger and larger. Which function eventually exceeds the other?\newline Choices:\newline(A)f(x)=8x+3.3(A)f(x) = 8x + 3.3\newline(B)g(x)=3.3x−5(B)g(x) = 3.3^x - 5
Get tutor helpright-arrow

Posted 8 months ago

Question
Both of these functions grow as x x gets larger and larger. Which function eventually exceeds the other?\newlineChoices:\newline(A) f(x)=2x+9(A) \ f(x) = 2x + 9 \newline(B) g(x)=2x(B)\ g(x) = 2^x
Get tutor helpright-arrow

Posted 8 months ago

Question
The functions f(x) f(x) and g(x) g(x) are differentiable. \newlineThe function h(x) h(x) is defined as: h(x)=g(x)f(x) h(x)=\frac{g(x)}{f(x)} \newlineIf f(8)=1 f(8)=1 , f′(8)=−6 f'(8)=-6 , g(8)=8 g(8)=8 , and g′(8)=−10 g'(8)=-10 , what is h′(8) h'(8) ? \newlineSimplify any fractions. \newlineh′(8)= h'(8)= ______
Get tutor helpright-arrow

Posted 8 months ago

Question
The functions p(x) p(x) and q(x) q(x) are differentiable. \newlineThe function r(x) r(x) is defined as: r(x)=p(x)q(x) r(x)= \frac{p(x)}{q(x)} \newlineIf p(3)=2 p(3)= 2 , p′(3)=4 p'(3)= 4 , q(3)=6 q(3)= 6 , and q′(3)=9 q'(3)= 9 , what is r′(3) r'(3) ? \newlineSimplify any fractions. \newliner′(3)= r'(3)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions u(x) u(x) and v(x) v(x) are differentiable. \newlineThe function w(x) w(x) is defined as: w(x)=u(x)v(x) w(x)= \frac{u(x)}{v(x)} \newlineIf u(5)=3 u(5)= 3 , u′(5)=−2 u'(5)= -2 , v(5)=7 v(5)= 7 , and v′(5)=1 v'(5)= 1 , what is w′(5) w'(5) ? \newlineSimplify any fractions. \newlinew′(5)= w'(5)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions a(x) a(x) and b(x) b(x) are differentiable. \newlineThe function c(x) c(x) is defined as: c(x)=a(x)b(x) c(x)= \frac{a(x)}{b(x)} \newlineIf a(2)=4 a(2)= 4 , a′(2)=5 a'(2)= 5 , b(2)=1 b(2)= 1 , and b′(2)=−3 b'(2)= -3 , what is c′(2) c'(2) ? \newlineSimplify any fractions. \newlinec′(2)= c'(2)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions m(x) m(x) and n(x) n(x) are differentiable. \newlineThe function o(x) o(x) is defined as: o(x)=m(x)n(x) o(x)= \frac{m(x)}{n(x)} \newlineIf m(7)=2 m(7)= 2 , m′(7)=−1 m'(7)= -1 , n(7)=4 n(7)= 4 , and n′(7)=8 n'(7)= 8 , what is o′(7) o'(7) ? \newlineSimplify any fractions. \newlineo′(7)= o'(7)= _____
Get tutor helpright-arrow

Posted 9 months ago

View all (345)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant