AI tutor
Full solution
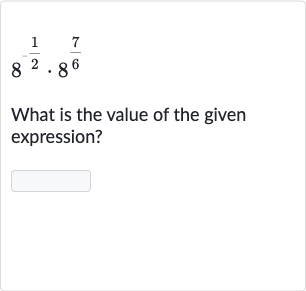
Q. What is the value of the given expression?
- Apply exponent property: Apply the property of exponents that states when multiplying expressions with the same base, you add the exponents.
- Add exponents: Add the exponents and together.
- Simplify the fraction: Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is .
- Substitute simplified exponent: Substitute the simplified exponent back into the base . simplifies to
- Calculate value of : Calculate the value of . Since , we can rewrite as .
- Calculate value of : Calculate the value of .
More problems from Compare linear, exponential, and quadratic growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help