Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

6^((1)/(6))*2^((5)/(6))*3^((7)/(6))
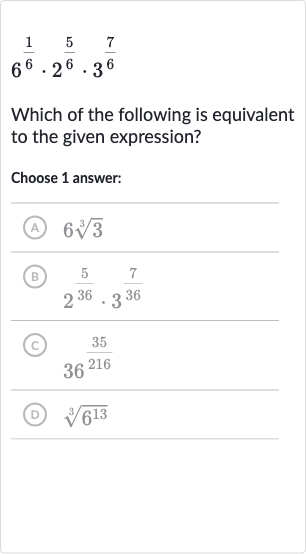
Which of the following is equivalent to the given expression?
Choose 1 answer:
(A)
6root(3)(3)
(B)
2^((5)/(36))*3^((7)/(36))
(C)
36^((35)/(216))
(D)
root(3)(6^(13))

$6^{\frac{1}{6}} \cdot 2^{\frac{5}{6}} \cdot 3^{\frac{7}{6}}$ $\newline$ Which of the following is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $6 \sqrt[3]{3}$ $\newline$ (B) $2^{\frac{5}{36}} \cdot 3^{\frac{7}{36}}$ $\newline$ (C) $36^{\frac{35}{216}}$ $\newline$ (D) $\sqrt[3]{6^{13}}$

View step-by-step help

View step-by-step help

Compare linear and exponential growth

Full solution

Q.

6^{\frac{1}{6}} \cdot 2^{\frac{5}{6}} \cdot 3^{\frac{7}{6}}

\newline

Which of the following is equivalent to the given expression?

\newline

Choose

1

answer:

\newline

(A)

6 \sqrt[3]{3}

\newline

(B)

2^{\frac{5}{36}} \cdot 3^{\frac{7}{36}}

\newline

(C)

36^{\frac{35}{216}}

\newline

(D)

\sqrt[3]{6^{13}}

Combine terms with same base: Combine the terms with the same base. $\newline$ We notice that $6$ can be written as $2 \times 3$ , so we can combine the terms with the base of $2$ and $3$ . $\newline$ $6^{(1/6)}\times2^{(5/6)}\times3^{(7/6)} = (2 \times 3)^{(1/6)}\times2^{(5/6)}\times3^{(7/6)}$
Apply exponent to factors: Apply the exponent to the factors of $6$ . $\newline$ $(2 \times 3)^{\frac{1}{6}} = 2^{\frac{1}{6}} \times 3^{\frac{1}{6}}$ $\newline$ Now we have all terms with base $2$ and $3$ , and we can combine them.
Combine exponents for base terms: Combine the exponents for the base $2$ and base $3$ terms. $\newline$ $2^{(1)/(6)} \times 2^{(5)/(6)} = 2^{(1)/(6) + (5)/(6)} = 2^1 = 2$ $\newline$ $3^{(1)/(6)} \times 3^{(7)/(6)} = 3^{(1)/(6) + (7)/(6)} = 3^{(8)/(6)} = 3^{4/3}$
Multiply simplified terms: Multiply the simplified terms. $2 \times 3^{\frac{4}{3}} = 2 \times \sqrt[3]{3^4} = 2 \times \sqrt[3]{81}$
Simplify cube root: Simplify the cube root. $\sqrt[3]{81} = 3^{4^{1/3}} = 3^{4/3} = 3^{1*4/3} = 3^{4/3} = 3 \times 3 = 9$
Multiply remaining terms: Multiply the remaining terms. $2 \times 9 = 18$
Check answer choices: Check the answer choices to see which one is equivalent to $18$ .
(A) $6\sqrt[3]{3}$ is not $18$ .
(B) $2^{\frac{5}{36}}\times3^{\frac{7}{36}}$ is not $18$ .
(C) $36^{\frac{35}{216}}$ is not $18$ .
(D) $\sqrt[3]{6^{13}}$ is not $18$ .
None of the answer choices are equivalent to $18$ , which means there might be a mistake in our calculations.

More problems from Compare linear and exponential growth

Question

Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits

x

days to pick up the motorcycle.

\newline

Write an equation for the function. If it is linear, write it in the form

g(x) = mx + b

. If it is exponential, write it in the form

g(x) = a(b)^x

\newline

g(x) = \underline{\hspace{3em}}

Posted 5 months ago

Question

f(t)=-2t-7

change over the interval from

t=-7

t=-6

\newline

\newline

\left[\text{f(t) decreases by } 2\right]

\newline

\left[\text{f(t) increases by } 2\right]

\newline

\left[\text{f(t) increases by } 200\%\right]

\newline

\left[\text{f(t) decreases by a factor of } 2\right]

Posted 5 months ago

Question

g(t)=9^t

change over the interval from

t=1

t=3

\newline

\newline

\left[\text{g(t) decreases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by } 18\%\right]

\newline

\left[\text{g(t) decreases by } 9\%\right]

Posted 5 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A)f(x) = 8x + 3.3

\newline

(B)g(x) = 3.3^x - 5

Posted 6 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A) \ f(x) = 2x + 9

\newline

(B)\ g(x) = 2^x

Posted 6 months ago

Question

f(x)

g(x)

are differentiable.

\newline

h(x)

h(x)=\frac{g(x)}{f(x)}

\newline

f(8)=1

f'(8)=-6

g(8)=8

g'(8)=-10

h'(8)

\newline

Simplify any fractions.

\newline

h'(8)=

Posted 6 months ago

Question

p(x)

q(x)

are differentiable.

\newline

r(x)

r(x)= \frac{p(x)}{q(x)}

\newline

p(3)= 2

p'(3)= 4

q(3)= 6

q'(3)= 9

r'(3)

\newline

Simplify any fractions.

\newline

r'(3)=

Posted 7 months ago

Question

u(x)

v(x)

are differentiable.

\newline

w(x)

w(x)= \frac{u(x)}{v(x)}

\newline

u(5)= 3

u'(5)= -2

v(5)= 7

v'(5)= 1

w'(5)

\newline

Simplify any fractions.

\newline

w'(5)=

Posted 7 months ago

Question

a(x)

b(x)

are differentiable.

\newline

c(x)

c(x)= \frac{a(x)}{b(x)}

\newline

a(2)= 4

a'(2)= 5

b(2)= 1

b'(2)= -3

c'(2)

\newline

Simplify any fractions.

\newline

c'(2)=

Posted 7 months ago

Question

m(x)

n(x)

are differentiable.

\newline

o(x)

o(x)= \frac{m(x)}{n(x)}

\newline

m(7)= 2

m'(7)= -1

n(7)= 4

n'(7)= 8

o'(7)

\newline

Simplify any fractions.

\newline

o'(7)=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant