Full solution
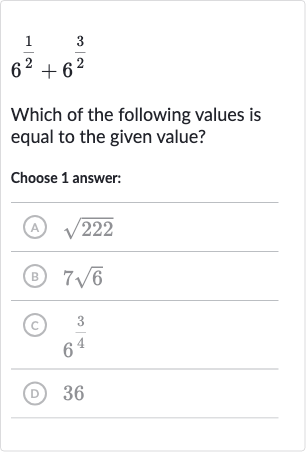
Q. Which of the following values is equal to the given value?Choose answer:(A) (B) (C) (D)
- Understanding the given expressions: Understand the given expressions. is the square root of , which can be written as . is the same as , which means the square root of cubed, or .
- Simplifying the expressions: Simplify the expressions. is already in its simplest form. means , which is because .
- Adding the simplified expressions: Add the simplified expressions..This can be written as , which is .
- Matching the result with the choices: Match the result with the given choices.The result from Step is , which corresponds to choice (B) .
More problems from Compare linear and exponential growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help