Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

((x^(2)y^(2)z^(2))^(5))/((x^(3)y^(3)z^(3))^(7)) Which of the following is equivalent to the given expression? Choose 1 answer: (A) (x^(-2)y^(-2)z^(-2))^(5)(x^(3)y^(3)z^(3))^(7) (B) (x^(5)y^(5)z^(5))^(2)(x^(-3)y^(-3)z^(-3))^(7) (c) ((x^(5)y^(5)z^(5))^(8))/((x^(7)y^(7)z^(7))^(27)) (D) ((x^(5)y^(5)z^(5))^(6))/((x^(7)y^(7)z^(7))^(9))

(x2y2z2)5(x3y3z3)7 \frac{\left(x^{2} y^{2} z^{2}\right)^{5}}{\left(x^{3} y^{3} z^{3}\right)^{7}} \newlineWhich of the following is equivalent to the given expression?\newlineChoose 11 answer:\newline(A) (x−2y−2z−2)5(x3y3z3)7 \left(x^{-2} y^{-2} z^{-2}\right)^{5}\left(x^{3} y^{3} z^{3}\right)^{7} \newline(B) (x5y5z5)2(x−3y−3z−3)7 \left(x^{5} y^{5} z^{5}\right)^{2}\left(x^{-3} y^{-3} z^{-3}\right)^{7} \newline(C) (x5y5z5)8(x7y7z7)27 \frac{\left(x^{5} y^{5} z^{5}\right)^{8}}{\left(x^{7} y^{7} z^{7}\right)^{27}} \newline(D) (x5y5z5)6(x7y7z7)9 \frac{\left(x^{5} y^{5} z^{5}\right)^{6}}{\left(x^{7} y^{7} z^{7}\right)^{9}}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Compare linear, exponential, and quadratic growthright chevron icon

Full solution

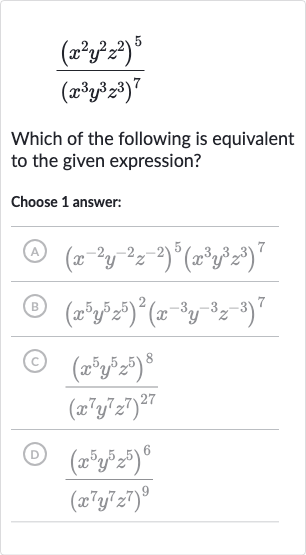
Q. (x2y2z2)5(x3y3z3)7 \frac{\left(x^{2} y^{2} z^{2}\right)^{5}}{\left(x^{3} y^{3} z^{3}\right)^{7}} \newlineWhich of the following is equivalent to the given expression?\newlineChoose 11 answer:\newline(A) (x−2y−2z−2)5(x3y3z3)7 \left(x^{-2} y^{-2} z^{-2}\right)^{5}\left(x^{3} y^{3} z^{3}\right)^{7} \newline(B) (x5y5z5)2(x−3y−3z−3)7 \left(x^{5} y^{5} z^{5}\right)^{2}\left(x^{-3} y^{-3} z^{-3}\right)^{7} \newline(C) (x5y5z5)8(x7y7z7)27 \frac{\left(x^{5} y^{5} z^{5}\right)^{8}}{\left(x^{7} y^{7} z^{7}\right)^{27}} \newline(D) (x5y5z5)6(x7y7z7)9 \frac{\left(x^{5} y^{5} z^{5}\right)^{6}}{\left(x^{7} y^{7} z^{7}\right)^{9}}
  1. Simplify Expression: Simplify the given expression using the properties of exponents.\newlineThe original expression is (x2y2z2)5(x3y3z3)7\frac{(x^{2}y^{2}z^{2})^{5}}{(x^{3}y^{3}z^{3})^{7}}.\newlineUsing the power of a product property, (a∗b)n=an∗bn(a*b)^{n} = a^{n} * b^{n}, we can rewrite the expression as:\newlinex2∗5y2∗5z2∗5x3∗7y3∗7z3∗7\frac{x^{2*5}y^{2*5}z^{2*5}}{x^{3*7}y^{3*7}z^{3*7}}.
  2. Apply Power Property: Now, simplify the exponents by multiplying them. x10y10z10x21y21z21\frac{x^{10}y^{10}z^{10}}{x^{21}y^{21}z^{21}}.
  3. Simplify Exponents: Next, apply the quotient of powers property, which states that anam=an−m\frac{a^n}{a^m} = a^{n-m}, to each variable separately.x10−21y10−21z10−21x^{10-21}y^{10-21}z^{10-21}.
  4. Apply Quotient Property: Subtract the exponents to simplify further. x(−11)y(−11)z(−11)x^{(-11)}y^{(-11)}z^{(-11)}.
  5. Subtract Exponents: The simplified expression is x−11y−11z−11x^{-11}y^{-11}z^{-11}, which can be rewritten using the negative exponent rule, a−n=1ana^{-n} = \frac{1}{a^n}, as:\newline1x11y11z11\frac{1}{x^{11}y^{11}z^{11}}.
  6. Rewrite with Negative Exponents: Now, let's compare the simplified expression with the answer choices.\newline(A) (x−2y−2z−2)5(x3y3z3)7(x^{-2}y^{-2}z^{-2})^{5}(x^{3}y^{3}z^{3})^{7} does not match our simplified expression.\newline(B) (x5y5z5)2(x−3y−3z−3)7(x^{5}y^{5}z^{5})^{2}(x^{-3}y^{-3}z^{-3})^{7} does not match our simplified expression.\newline(C) ((x5y5z5)8)/((x7y7z7)27)((x^{5}y^{5}z^{5})^{8})/((x^{7}y^{7}z^{7})^{27}) does not match our simplified expression.\newline(D) ((x5y5z5)6)/((x7y7z7)9)((x^{5}y^{5}z^{5})^{6})/((x^{7}y^{7}z^{7})^{9}) does not match our simplified expression.\newlineNone of the answer choices match the simplified expression 1/(x11y11z11)1/(x^{11}y^{11}z^{11}).

More problems from Compare linear, exponential, and quadratic growth

Question
Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits xx days to pick up the motorcycle.\newlineWrite an equation for the function. If it is linear, write it in the form g(x)=mx+bg(x) = mx + b. If it is exponential, write it in the form g(x)=a(b)xg(x) = a(b)^x.\newlineg(x)=‾g(x) = \underline{\hspace{3em}}
Get tutor helpright-arrow

Posted 8 months ago

Question
How does f(t)=−2t−7f(t)=-2t-7 change over the interval from t=−7t=-7 to t=−6t=-6?\newlineChoices:\newline[f(t) decreases by 2]\left[\text{f(t) decreases by } 2\right]\newline[f(t) increases by 2]\left[\text{f(t) increases by } 2\right]\newline[f(t) increases by 200%]\left[\text{f(t) increases by } 200\%\right]\newline[f(t) decreases by a factor of 2]\left[\text{f(t) decreases by a factor of } 2\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
How does g(t)=9tg(t)=9^t change over the interval from t=1t=1 to t=3t=3?\newlineChoices: \newline[g(t) decreases by a factor of 81]\left[\text{g(t) decreases by a factor of } 81\right]\newline[g(t) increases by a factor of 81]\left[\text{g(t) increases by a factor of } 81\right]\newline[g(t) increases by 18%]\left[\text{g(t) increases by } 18\%\right]\newline[g(t) decreases by 9%]\left[\text{g(t) decreases by } 9\%\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
Both of these functions grow as xx gets larger and larger. Which function eventually exceeds the other?\newline Choices:\newline(A)f(x)=8x+3.3(A)f(x) = 8x + 3.3\newline(B)g(x)=3.3x−5(B)g(x) = 3.3^x - 5
Get tutor helpright-arrow

Posted 9 months ago

Question
Both of these functions grow as x x gets larger and larger. Which function eventually exceeds the other?\newlineChoices:\newline(A) f(x)=2x+9(A) \ f(x) = 2x + 9 \newline(B) g(x)=2x(B)\ g(x) = 2^x
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions f(x) f(x) and g(x) g(x) are differentiable. \newlineThe function h(x) h(x) is defined as: h(x)=g(x)f(x) h(x)=\frac{g(x)}{f(x)} \newlineIf f(8)=1 f(8)=1 , f′(8)=−6 f'(8)=-6 , g(8)=8 g(8)=8 , and g′(8)=−10 g'(8)=-10 , what is h′(8) h'(8) ? \newlineSimplify any fractions. \newlineh′(8)= h'(8)= ______
Get tutor helpright-arrow

Posted 8 months ago

Question
The functions p(x) p(x) and q(x) q(x) are differentiable. \newlineThe function r(x) r(x) is defined as: r(x)=p(x)q(x) r(x)= \frac{p(x)}{q(x)} \newlineIf p(3)=2 p(3)= 2 , p′(3)=4 p'(3)= 4 , q(3)=6 q(3)= 6 , and q′(3)=9 q'(3)= 9 , what is r′(3) r'(3) ? \newlineSimplify any fractions. \newliner′(3)= r'(3)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions u(x) u(x) and v(x) v(x) are differentiable. \newlineThe function w(x) w(x) is defined as: w(x)=u(x)v(x) w(x)= \frac{u(x)}{v(x)} \newlineIf u(5)=3 u(5)= 3 , u′(5)=−2 u'(5)= -2 , v(5)=7 v(5)= 7 , and v′(5)=1 v'(5)= 1 , what is w′(5) w'(5) ? \newlineSimplify any fractions. \newlinew′(5)= w'(5)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions a(x) a(x) and b(x) b(x) are differentiable. \newlineThe function c(x) c(x) is defined as: c(x)=a(x)b(x) c(x)= \frac{a(x)}{b(x)} \newlineIf a(2)=4 a(2)= 4 , a′(2)=5 a'(2)= 5 , b(2)=1 b(2)= 1 , and b′(2)=−3 b'(2)= -3 , what is c′(2) c'(2) ? \newlineSimplify any fractions. \newlinec′(2)= c'(2)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions m(x) m(x) and n(x) n(x) are differentiable. \newlineThe function o(x) o(x) is defined as: o(x)=m(x)n(x) o(x)= \frac{m(x)}{n(x)} \newlineIf m(7)=2 m(7)= 2 , m′(7)=−1 m'(7)= -1 , n(7)=4 n(7)= 4 , and n′(7)=8 n'(7)= 8 , what is o′(7) o'(7) ? \newlineSimplify any fractions. \newlineo′(7)= o'(7)= _____
Get tutor helpright-arrow

Posted 9 months ago

View all (100)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant